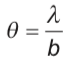Homework Help Overview
The discussion revolves around the relationship between distance and angle in the context of double slit interference, specifically examining the formula used to calculate distances between interference maxima and minima. Participants are exploring the implications of the formula and its application to a given problem.
Discussion Character
- Conceptual clarification, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants are attempting to understand the formula for distance between maxima and minima, questioning why a multiplication factor is needed in their calculations. There is also exploration of the definitions of angles in relation to maxima and minima in interference patterns.
Discussion Status
The discussion is active, with participants providing clarifications about the formula and its application. Some are questioning the assumptions made in the problem setup and exploring the meaning of angles in the context of the interference pattern.
Contextual Notes
There is mention of confusion regarding the definitions of distance and angle in the context of double slit interference and diffraction grating, indicating potential gaps in understanding the problem requirements.