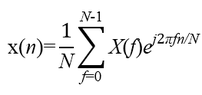What Is the Relation Between \( x(n) \) and \( X(f) \) Given \( f = kn \)?

  • Context: MHB 
  • Thread starter Thread starter maysam1
  • Start date Start date
  • Tags Tags
    Fft Transform
Click For Summary
SUMMARY

The discussion centers on the relationship between discrete time signals \( x(n) \) and their frequency domain representation \( X(f) \) through the Discrete Fourier Transform (DFT). It is established that when a linear relationship \( f = kn \) exists, where \( k \) is a constant, this implies a direct correlation between time and frequency within a specific system. The example provided involves the signal \( x(n) = c \cdot n \), indicating that the DFT can be computed for linear time-dependent signals.

PREREQUISITES
  • Understanding of Discrete Fourier Transform (DFT)
  • Knowledge of signal processing concepts
  • Familiarity with linear relationships in mathematical functions
  • Basic grasp of discrete time signals
NEXT STEPS
  • Study the mathematical derivation of the DFT for linear signals
  • Explore the implications of linear time-frequency relationships in signal processing
  • Learn about the properties of DFT and its applications in real-world signals
  • Investigate the effects of different constants \( k \) on frequency representation
USEFUL FOR

Students and professionals in signal processing, electrical engineering, and anyone interested in understanding the transformation of discrete time signals to their frequency domain representations.

maysam1
Messages
3
Reaction score
0
Suppose that there is a linear relation between discrete time (n) and frequency (f), then what is the relatian between x(n) and X(f) (X(f) is DFT transform of x(n))?
 
Last edited:
Physics news on Phys.org
maysam said:
Suppose that there is a linear relation between discrete time (n) and frequency (f), then what is the relatian between x(n) and X(f) (X(f) is DFT transform of x(n))?

Hi maysam! Welcome to MHB! (Smile)

I guess we'll need to find the DFT transform of $x(n)=c\cdot n$ where $c$ is some constant.
Can you calculate it?
What is the formula for a DFT?
 
I like Serena said:
Hi maysam! Welcome to MHB! (Smile)

I guess we'll need to find the DFT transform of $x(n)=c\cdot n$ where $c$ is some constant.
Can you calculate it?
What is the formula for a DFT?

Hi, x(n) can be any signal.
 

Attachments

  • Capture.PNG
    Capture.PNG
    1.8 KB · Views: 116
maysam said:
Hi, x(n) can be any signal.

Hmm... can you clarify what a "linear relation between discrete time (n) and frequency (f)" means?

Presumably we have a signal amplitude $x(n) = x(t_n)$ that depends on time, which transforms to a signal amplitude $X(f) = X(f_k)$ that depends on frequency.
There is no relation between time and frequency.
 
I like Serena said:
Hmm... can you clarify what a "linear relation between discrete time (n) and frequency (f)" means?

Presumably we have a signal amplitude $x(n) = x(t_n)$ that depends on time, which transforms to a signal amplitude $X(f) = X(f_k)$ that depends on frequency.
There is no relation between time and frequency.

Yes, originally There is no relation between time and frequency but In a system we can assume that f=kn and k is a constant. this means that in this system we can see a linear relation between time and frequency.
 

Similar threads

Is my understanding of the Nyquist theorem correct?
  • · Replies 4 ·
Replies
4
Views
2K
Graduate Functional equation f(x)^n f(a - x) = 1
  • · Replies 4 ·
Replies
4
Views
2K
MHB Understanding Picard Iteration: What Does ${f}^{n}x \subseteq {f}^{n+1}x$ Mean?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Image of each open subset is open
  • · Replies 4 ·
Replies
4
Views
2K
MHB Is $f_n(x_n) \to f(x)$ Given $f_n \to f$ Uniformly and $x_n \to x$?
  • · Replies 2 ·
Replies
2
Views
2K
Proving that there exists a solution to ##f(x+\frac1n)-f(x)=0##
  • · Replies 4 ·
Replies
4
Views
1K
What is the Difference Between FFT Scaling and Analytical Fourier Transform?
  • · Replies 26 ·
Replies
26
Views
5K
Wavelet transform (CWT and DWT)
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad What is the difference between these two power series theorems?
  • · Replies 5 ·
Replies
5
Views
3K
MHB Help for test - functional analysis
  • · Replies 5 ·
Replies
5
Views
4K