Bishop556
- 37
- 4
Note that the code I am using is Python. Currently, I am attempting to numerically solve the equations of state that give rise to the Chandrasekar limit for a white dwarf star. My code works for a simple harmonic oscillator given the correct equations of motion, but does not compute the correct curve for my two coupled ODEs that I need for my project. My code is below. Note that the equations of state are defined in the comments.
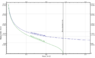
For some reason when I run this all I receive is a straight linear line which is nothing like the curve I expected that is attached to this post. Also, the graph indicates my mass is negative which is ridiculous. I have a feeling the error is a semantic error somewhere in my code, but would I not expect a curve instead of a straight line for ODEs that are obviously not linear. Thanks again.
EDIT: I forgot to mention that what the curve should resemble is the curve in the relativistic fermi gas line.
Python:
import numpy as np
import matplotlib.pyplot as plt
from math import sqrt
#Variable Definitions
N = 500 #number of entries
dur = 25000 #radius taken up to in kilometers
dr = dur / float(N-1) #step size
#creating the array
y = np.zeros([N,2])
y[0,0] = 20 #initial central momentum
y[0,1] = 0 #initial mass
#runge kutta algorithm
def rk4(y, r, dr, deriv):
k1 = dr * deriv(y,r)
k2 = dr * deriv(y + 0.5*k1,r + 0.5*dr)
k3 = dr * deriv(y + 0.5*k2, r + 0.5*dr)
k4 = dr * deriv(y + k3, r + dr)
y_next = y + (k1 + 2*(k2+k3)+k4)/6
return y_next#Equations of state (Note that x[0] is my fermi momentum x and x[1] is my mass. r is my radius
def Eqns(x,r):
y0 = (-5*x[1]*sqrt(1+x[0]**2))/(3*x[0]*r**2) #dx/dr = -5/3(M/r^2)*sqrt(1+x^2)/x
y1 = 3*(r**2)*(x[0]**3) #dM/dr = 3*r^2*x^3
return np.array([y0,y1])
#forming data points
for i in range(N-1):
y[i+1] = rk4(y[i],10**(-23), dr, Eqns) #started at some arbitrary smalll value to avoid
#singularity
radius = np.linspace(10**(-23),25000, N)
#plotting
plt.plot(y[:,1],radius)
plt.show()For some reason when I run this all I receive is a straight linear line which is nothing like the curve I expected that is attached to this post. Also, the graph indicates my mass is negative which is ridiculous. I have a feeling the error is a semantic error somewhere in my code, but would I not expect a curve instead of a straight line for ODEs that are obviously not linear. Thanks again.
EDIT: I forgot to mention that what the curve should resemble is the curve in the relativistic fermi gas line.
Attachments
Last edited by a moderator: