What is the Tension in the Wire for a Mass Pulled on a Rotating Disc?

[Karol]

Homework Statement

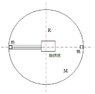
A disc of radius R and mass M lays on a smooth table. a smooth channel is carved along the diameter and on both ends there are masses m. one of the masses is attached with a wire to a small, almost weightless motor that is in the center. the other mass remains fixed in place. the disc can rotate round it's center using a smooth nail.
At t=0 the disc rotates at ω₀ and the motor starts pulling the left mass with acceleration a₀. what is the tension in the wire.
Now the nail is removed and at t=0 the disc again rotates at ω₀ and the motor running. find the distance s(t) of the center of mass of the system relative to the center.
What is the angular velocity of the disc as a function of time. use s(t).
What is the tension in the wire at t=0

Homework Equations

Centrifugal force: $F=m\frac{v^2}{R}$
Moment of inertia of a disc: $I=\frac{1}{2}MR^2$
Distance with constant acceleration: $s=\frac{1}{2}at^2$

The Attempt at a Solution

The tension at t=0 with the nail is the centripetal force+force due to linear acceleration:
$$F=m(\omega_0^2R+a_0)$$
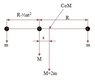
Moments round the left, moving, mass gives the C.O.M. distance s(t):
$$m\left( R+\frac{1}{2}at_0^2 \right)+M\left( \frac{1}{2}at_0^2 \right)=(M+m)\left( \frac{1}{2}at_0^2+s \right)$$
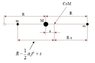
$$\rightarrow s(t)=\frac{a_0 t^2}{4}$$
The angular velocity ω without the nail is from conservation of angular momentum.
I consider, for the last term on the right side of the equation, the distance of each mass from the new C.O.M.
$$\frac{1}{2}M\omega_0^2 R^2+2mR^2\omega_0^2=\frac{1}{2}M\omega^2+2m\left( \frac{R+s(t)}{2} \right)^2$$
$$\omega_0^2 R^2 \left( \frac{M}{2}+2m \right)=\omega^2\left( \frac{M}{2}R^2+2m\left( \frac{R+s(t)}{2} \right)^2 \right)$$
I think the tension force at this situation is similar to the first when the nail was.

 

[SammyS]

 

[Nathanael]

I'm a bit confused: if the motor is on the disc, why would the CoM move when the nail is removed?

 

[Karol]

I'm a bit confused: if the motor is on the disc, why would the CoM move when the nail is removed?

The CoM doesn't move when we remove the nail, i am asked about the distance of the CoM from the center.

 

[Nathanael]

The CoM doesn't move when we remove the nail, i am asked about the distance of the CoM from the center.

Okay. By "center" you mean the center of the disk right?

and the motor starts pulling the left mass with acceleration a₀

I take it a₀ is constant the whole time?

There seems to be two interpretations of what a₀ could mean. (Maybe someone can point out why one is more reasonable.)
One interpretation, which you took, is that $a_0=\ddot r$
The other interpretation is that a₀ is the total radial acceleration (that is, it includes the centripetal acceleration).

From the first interpretation, we get your equation, $F_{tension}=m(\omega ^2R+a_0)$
From the second interoperation, the tension is more trivial, $F_{tension}=ma_0$

But for s(t), the second interpretation makes it much more interesting because $\ddot r$ is not constant.Anyway sorry for responding without properly looking at your work, but I have to go to a jazz thing for music class. I'll be back later if the problem is not cleared up by then.

[edited to fix latex]

 

[haruspex]

Moments round the left, moving, mass gives the C.O.M. distance s(t):

You cannot take angular momentum to be conserved about an accelerating reference point.
As Nathanael notes, taking a₀ to be relative to the groove makes finding s(t) simple. Just consider that the mass centre of the system is fixed, and calculate that mass centre from the known relative positions of the three objects at time t.

There seems to be two interpretations of what a₀ could mean. (Maybe someone can point out why one is more reasonable.)

Since the question asks for the tension in both contexts, it seems the acceleration should be taken as relative to the groove.

 

[Karol]

The acceleration a₀ is relative to the groove.

taking a₀ to be relative to the groove makes finding s(t) simple. Just consider that the mass centre of the system is fixed, and calculate that mass centre from the known relative positions of the three objects at time t.

The CoM is the origin.
$$\frac{m(R-s)-Ms-m\left[ \left( R-\frac{1}{2}a_0t^2 \right) +s \right] }{M+2m}=0\;\rightarrow\; s=\frac{\frac{1}{2}a_0t^2}{M+2m}$$

 

[haruspex]

The acceleration a₀ is relative to the groove.

The CoM is the origin.
$$\frac{m(R-s)-Ms-m\left[ \left( R-\frac{1}{2}a_0t^2 \right) +s \right] }{M+2m}=0\;\rightarrow\; s=\frac{\frac{1}{2}a_0t^2}{M+2m}$$

You seem to have dropped a factor at the final step. (Checking dimensional consistency is a useful habit.)

 

[Karol]

$$\frac{m(R-s)-Ms-m\left[ \left( R-\frac{1}{2}a_0t^2 \right) +s \right] }{M+2m}=0\;\rightarrow\; s=\frac{\frac{1}{2}ma_0t^2}{M+2m}$$
If this correct let's continue

 

[haruspex]

$$\frac{m(R-s)-Ms-m\left[ \left( R-\frac{1}{2}a_0t^2 \right) +s \right] }{M+2m}=0\;\rightarrow\; s=\frac{\frac{1}{2}ma_0t^2}{M+2m}$$
If this correct let's continue

Yes, I believe that is right.

 

[Karol]

So is the rest true? i mean does the angular velocity follow what i have written in the OP:

The angular velocity ω without the nail is from conservation of angular momentum.
I consider, for the last term on the right side of the equation, the distance of each mass from the new C.O.M.
$$\frac{1}{2}M\omega_0^2 R^2+2mR^2\omega_0^2=\frac{1}{2}M\omega^2+2m\left( \frac{R+s(t)}{2} \right)^2$$
$$\omega_0^2 R^2 \left( \frac{M}{2}+2m \right)=\omega^2\left( \frac{M}{2}R^2+2m\left( \frac{R+s(t)}{2} \right)^2 \right)$$
I think the tension force at this situation is similar to the first when the nail was.

 

[haruspex]

So is the rest true? i mean does the angular velocity follow what i have written in the OP:

There seem to be a few problems with the expression for the angular momentum at time t.
The first term is missing any radius factor, and I see no alowance for the fact that the disc is not rotating about its own centre.
I also think the 'm' term is wrong. Safer to consider each mass separately.

 

[Karol]

The disc's moment of inertia after the nail is removed-shteiner's theorem: $I_M=\frac{1}{2}MR^2+Ms^2$
$$\frac{1}{2} M \omega_0^2 R^2+2mR^2 \omega_0^2=\omega^2 \left\{ \frac{1}{2}MR^2+Ms^2+m\left[ ( R-s)^2+\left( R-\frac{1}{2}a_0t^2+s^2 \right)^2 \right] \right\}$$

 

[haruspex]

The disc's moment of inertia after the nail is removed-shteiner's theorem: $I_M=\frac{1}{2}MR^2+Ms^2$
$$\frac{1}{2} M \omega_0^2 R^2+2mR^2 \omega_0^2=\omega^2 \left\{ \frac{1}{2}MR^2+Ms^2+m\left[ ( R-s)^2+\left( R-\frac{1}{2}a_0t^2+s^2 \right)^2 \right] \right\}$$

Looks right except for a typo... an extra power of 2 on the last occurrence of s.

 

[Karol]

Thanks.
$$\frac{1}{2} M \omega_0^2 R^2+2mR^2 \omega_0^2=\omega^2 \left\{ \frac{1}{2}MR^2+Ms^2+m\left[ ( R-s)^2+\left( R-\frac{1}{2}a_0t^2+s \right)^2 \right] \right\}$$
But what about the last part, what is the tension in the wire? i don't have a clue so i think it should be the same as when the nail was.

 

[haruspex]

Thanks.
$$\frac{1}{2} M \omega_0^2 R^2+2mR^2 \omega_0^2=\omega^2 \left\{ \frac{1}{2}MR^2+Ms^2+m\left[ ( R-s)^2+\left( R-\frac{1}{2}a_0t^2+s \right)^2 \right] \right\}$$
But what about the last part, what is the tension in the wire? i don't have a clue so i think it should be the same as when the nail was.

Not sure, but where it says "use s(t)" it might mean that the answer should not reference t directly at all. You can replace t using s. Some simplification may then be possible.
Wrt tension, I think you could consider what the tension would be without rotation and then add the centripetal force.

 

[Karol]

Wrt tension, I think you could consider what the tension would be without rotation and then add the centripetal force.

I consider the non-inertial frame of the accelerating disk. s is the distance of the CoM from the center. the CoM remains in place so the disk with the masses on it accelerate to the left with acceleration:
$$s=\frac{\frac{1}{2}a_0t^2}{M+2m}=\frac{ma_0t^2}{2(M+m)}\;\rightarrow\; \ddot s=\frac{ma_0}{M+2m}$$
The total tension force:
$$F=m\frac{ma_0}{M+2m}+m\omega_0^2R$$

 

[haruspex]

I consider the non-inertial frame of the accelerating disk. s is the distance of the CoM from the center. the CoM remains in place so the disk with the masses on it accelerate to the left with acceleration:
$$s=\frac{\frac{1}{2}a_0t^2}{M+2m}=\frac{ma_0t^2}{2(M+m)}\;\rightarrow\; \ddot s=\frac{ma_0}{M+2m}$$
The total tension force:
$$F=m\frac{ma_0}{M+2m}+m\omega_0^2R$$

The tension is accelerating the mass relative to the disk. $\ddot s$ is the acceleration of the disk.

 

[Karol]

The tension is accelerating the mass relative to the disk. $\ddot s$ is the acceleration of the disk.

It's dalamber's force in an accelerated system, don't i have to add it? if that's correct then i only have to add the force due a₀
$$F=m\frac{ma_0}{M+2m}+m\omega_0^2R+ma_0$$

 

[haruspex]

It's dalamber's force in an accelerated system, don't i have to add it? if that's correct then i only have to add the force due a₀
$$F=m\frac{ma_0}{M+2m}+m\omega_0^2R+ma_0$$

Aren't $\ddot s$ and $a_0$ in opposite directions?

 

[Karol]

Aren't $\ddot s$ and $a_0$ in opposite directions?

$$F=m\omega_0^2R+ma_0-m\frac{ma_0}{M+2m}$$

 

[haruspex]

$$F=m\omega_0^2R+ma_0-m\frac{ma_0}{M+2m}$$

That looks good.

 

[Karol]

Thanks very (very) much