Dustinsfl
- 2,217
- 5
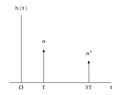
In a long-distance telephone communication, an echo is sometimes encountered due to the transmitted signal being reflected at the receiver, sent back down the line, reflected again at the transmitter, and returned to the receiver. The impulse response for a system that modles this effect is shown in figure, where we have assumed tat only one echo is received. The parameter \(T\) corresponds to the one-way travel time along the communication channel, and the parameter \(\alpha\) represents the attenuation in amplitude between transmitter and receiver.
View attachment 2099
Determine the system function \(H(s)\) and associated region of convergence for the system.
How can I determine a transfer function from this?
View attachment 2099
Determine the system function \(H(s)\) and associated region of convergence for the system.
How can I determine a transfer function from this?