- #1
H Smith 94
Gold Member
- 55
- 1
Before I start, I apologise for the information dump that is to follow. I don't expect all questions to be answered or all models to be addressed; I simply feel it is appropriate to provide the community with my current knowledge and stage of research so you may not have to search for it yourselves in order to begin a discussion. It also might help some to find a consolidated resource regarding this subject (I know it would have helped me!)
From the very limited literature I can find regarding radio waves in saline-water solutions (as in seawater), I have been able to find very few corroborating models of radio wave propagation through electrically lossy media. I have found the following descriptions, which I have paraphrased here and adapted.
My questions
My primary questions here are:
Note that I have "boxed" the final equations of each model to ease reading.
Ghasemi's (2012) theoretical model
Power flux density
According to Friis' transmission equation, the received power flux density ##P_r## is given by
\begin{equation}P_r=P_t G_t G_r \left(\frac{λ}{4πr}\right)^2,\end{equation}
where ##P_t## is the transmitted power flux density; ##G_t## and ##G_r## are the gain of the transmission antenna and the receiving antenna, respectively; and ##r## is the distance between the two antenna.
Since ##λ=c/f##, where ##c## is the speed of light within the medium and ##c=c_0/n##, where ##n## is the refractive index of the medium and ##c_0## is the speed of light in free space. Thus,
\begin{equation}P_r=P_t G_t G_r \left(\frac{c_0}{4πrnf}\right)^2.\end{equation}
If salinity is ##S## and the resulting change in refractive index is ##\Delta n##, then it may be empirically determined that ##S=0.2\,\Delta n##, so if ##n=n_\text{water}+\Delta n## then ##n=n_\text{water}+\frac{S}{0.2}##.
Now, since ##n_\text{water} =1.3330##,
\begin{equation}P_r=P_t G_t G_r \left(\frac{c_0}{4πrf}\frac{0.2}{0.267+S}\right)^2.\end{equation}
Using the https://www.itu.int/dms_pubrec/itu-r/rec/v/R-REC-V.573-5-200709-I!PDF-E.pdf (pg. 6) ##L##, which states that
\begin{equation}L = 10 \log\left|\frac{P_t}{P_r}\right|\end{equation}
we find that,
\begin{equation}\begin{split}L &= -10 \log\left|P_r/P_t\right|\\&= -10 \log\left|G_t G_R \left(\frac{c_0}{4πrf}\frac{0.2}{0.267+S}\right)^2 \right|.\end{split}\end{equation}
This model is according to Ghasemi's Propagation Engineering in Wireless Communications (2012, pp. 37-39) and has been adapted to incorporate salinity.
Using this further, we find that
\begin{equation}\boxed{L_\text{total} = \text{FSL}\,[\text{dB}] + L_m\,[\text{dB}] − G_t \,[\text{dB}] − G_r \,[\text{dB}]}.\end{equation}
where ##\text{FSL}## is the free space loss given by
\begin{equation}\text{FSL}\,[\text{dB}] = 20 \log\left|\frac{4πrf}{c_0}\frac{0.267+S}{0.2}\right|\end{equation}
and ##L_m## is the loss within the medium (undefined by Ghasemi.)
Depth of penetration
If we define depth of penetration as ##x\equiv1/\alpha##, where ##\alpha = \sqrt{\pi\mu\sigma f}## is the attenuation, so
\begin{equation}\begin{split}x&=\frac{1}{\sqrt{\pi\mu\sigma f}}\\&=\frac{1}{\sqrt{\pi\mu_0}}\cdot\frac{1}{\sqrt{\mu_r\sigma f}}\\&=892.0621\frac{1}{\sqrt{\mu_r\sigma f}}.\end{split}\end{equation}
Now, "for all practical purposes the relative permeability of salt water is 1," (Herring, 2007) so:
\begin{equation}\boxed{x=892.0621\frac{1}{\sqrt{\sigma f}}}.\end{equation}
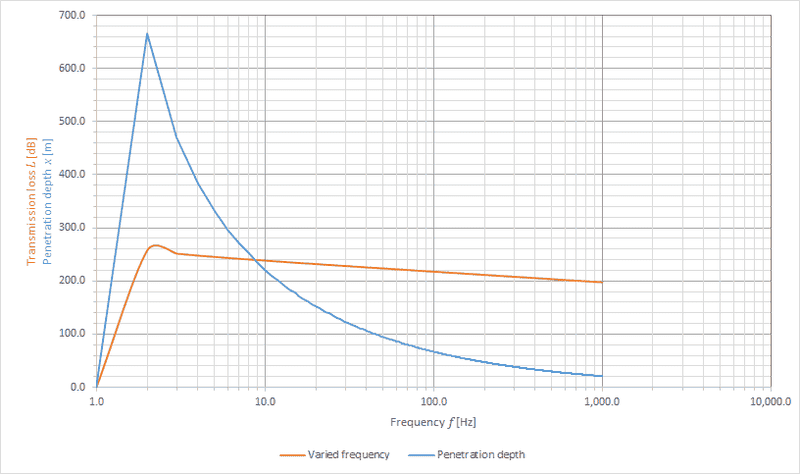
The above is a simulation (using Excel) of the model, showing the penetration depth and absolute transmission loss as a function of frequency. Here we witness the penetration depth holding true to our expectations—if perhaps a little more extreme than expected—and the transmission loss showing the *opposite* of what the penetration depth shows.
Zoksimovski (2012) semi-empirical model
I did find a good experimental report, Underwater Electromagnetic Communications Using
Conduction – Channel Characterization (Zoksimovski et. al., 2012), which detailed three separate approximate models for radio wave attenuation using a channel transfer function ##H##, outlining two far-field approximations:
\begin{equation}|H| = A_0 e^{-\alpha_1\sqrt{f}} \ \ \ \ \ \ \ (1)\end{equation}
\begin{equation}|H| = A_0 e^{-\alpha_2 f} \ \ \ \ \ \ \ \ \ (2)\end{equation}
and a near-field approximation:
\begin{equation} \boxed{|H| = \frac{p_1f^2 + p_2f + p_3}{q_1f^2 + q_2f + q_3}\,e^{-\alpha_3 f}}.\end{equation}
I'm interested more-so in the near field due to the high observed attenuation of radio waves in seawater. The data provided by Zoksimovski et. al. was unclear at best, but averages were found to be ##p_1 = 0.75\times 10^{-5}##, ##p_2 = 2.30\times 10^{-4}##, ##p_3 = 17.25\times 10^{-5}##, ##q_1 = 0.30##, ##q_2 = 0.15##, ##q_3 = 0.18##, ##\alpha_3 = 0.55##. These were the values used in the following simulation.
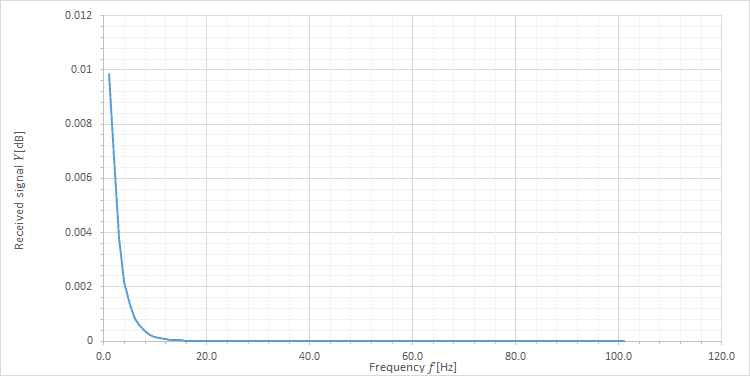
As you can see this model produces *tiny* received signals which are killed off within 10 Hz. I know this to not be physically accurate. It also does not factor the distance between antenna anywhere into calculations.
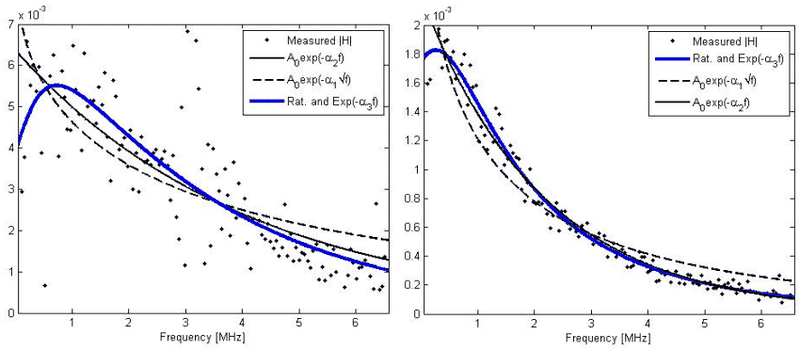
This is the graphs produced by Zoksimovski et. al. which do not show the same trends as my simulation (see the thick blue lines for the model discussed.) Perhaps this is an error in my simulation, however intuition suggests that the low values of the parameters will influence the trend in the way I've simulated.
Cole-Cole Relation
The Cole-Cole relation—and its specialisation, the Debye relaxation model—was brought to my attention by O'Shaugnessy's 2012 brilliant paper, Characterising the Relative Permittivity and Conductivity of Seawater for Electromagnetic Communications in the Radio Band.
The Cole-Cole relation states that
\begin{equation} \hat{\epsilon}(\omega) = \epsilon_\infty + \frac{\Delta\epsilon}{1+(j\omega\tau)^{1-\alpha}} \end{equation}
where ##\hat{\epsilon}(\omega)## is the complex permittivity, ##\hat{\epsilon}(\omega) = \epsilon' + j\epsilon''##; ##\Delta\epsilon = \epsilon_s- \epsilon_\infty##, where ##\epsilon_s## is the static permittivity and ##\epsilon_\infty## is the infinite frequency permittivity; ##\omega = 2\pi f##; ##\tau## is the dielectric relaxation time; ##j = \sqrt{-1}##; and ##\alpha## is used to describe the spectral shape:
\begin{equation} \epsilon_r = \epsilon_\infty + \frac{\Delta\epsilon}{1 + j\frac{\omega\epsilon}{\sigma}} - j\frac{\sigma}{\omega\epsilon_0}, \end{equation}
where ##\sigma## is the conductivity of the medium.
I'll be honest, I don't fully understand this model, but I appreciate that it attempts to address the dependence of the relative permittivity on frequency. This seems like an important point.
Could anyone perhaps explain this model? How could this be applied into a model for radio propagation? Also, I'm still finding difficulty understanding the application of complex numbers in electromagnetism (such as in wave phase): how does it translate into real terms? It also appears in the following propagation model.
O'Shaugnessy's (2012) Dielectric Propagation Model
Again, this model is from Characterising the Relative Permittivity and Conductivity of Seawater for Electromagnetic Communications in the Radio Band (O'Shaugnessy's, 2012). It states that:
\begin{equation}\boxed{E_z = E_{0, z} e^{j\omega t - \gamma z}} \ \ \ \ ,\ \ \ \ \boxed{H_z = H_{0, z} e^{j\omega t - \gamma z}} \end{equation}
where ##E## represents the electric field strength, ##H## the magnetic field strength and
\begin{equation} \gamma_{\text{water}}=\alpha + j\beta = j\omega\sqrt{\mu\left( \epsilon - j \frac{\sigma}{\omega}. \right)} \end{equation}
The author then continues to discuss the conduction and dielectric bands of this model depending on the relationship between ##\frac{\sigma}{\omega}## and ##\epsilon##.
Could anyone help to explain this?
From the very limited literature I can find regarding radio waves in saline-water solutions (as in seawater), I have been able to find very few corroborating models of radio wave propagation through electrically lossy media. I have found the following descriptions, which I have paraphrased here and adapted.
My questions
My primary questions here are:
- What models of radio wave propagation currently exist?
- How do these models apply to propagation and attenuation through salt-water solutions and seawater?
- What are the errors and successes with the models I have provided?
- Where does my understanding/knowledge falter?
Note that I have "boxed" the final equations of each model to ease reading.
Ghasemi's (2012) theoretical model
Power flux density
According to Friis' transmission equation, the received power flux density ##P_r## is given by
\begin{equation}P_r=P_t G_t G_r \left(\frac{λ}{4πr}\right)^2,\end{equation}
where ##P_t## is the transmitted power flux density; ##G_t## and ##G_r## are the gain of the transmission antenna and the receiving antenna, respectively; and ##r## is the distance between the two antenna.
Since ##λ=c/f##, where ##c## is the speed of light within the medium and ##c=c_0/n##, where ##n## is the refractive index of the medium and ##c_0## is the speed of light in free space. Thus,
\begin{equation}P_r=P_t G_t G_r \left(\frac{c_0}{4πrnf}\right)^2.\end{equation}
If salinity is ##S## and the resulting change in refractive index is ##\Delta n##, then it may be empirically determined that ##S=0.2\,\Delta n##, so if ##n=n_\text{water}+\Delta n## then ##n=n_\text{water}+\frac{S}{0.2}##.
Now, since ##n_\text{water} =1.3330##,
\begin{equation}P_r=P_t G_t G_r \left(\frac{c_0}{4πrf}\frac{0.2}{0.267+S}\right)^2.\end{equation}
Using the https://www.itu.int/dms_pubrec/itu-r/rec/v/R-REC-V.573-5-200709-I!PDF-E.pdf (pg. 6) ##L##, which states that
\begin{equation}L = 10 \log\left|\frac{P_t}{P_r}\right|\end{equation}
we find that,
\begin{equation}\begin{split}L &= -10 \log\left|P_r/P_t\right|\\&= -10 \log\left|G_t G_R \left(\frac{c_0}{4πrf}\frac{0.2}{0.267+S}\right)^2 \right|.\end{split}\end{equation}
This model is according to Ghasemi's Propagation Engineering in Wireless Communications (2012, pp. 37-39) and has been adapted to incorporate salinity.
Using this further, we find that
\begin{equation}\boxed{L_\text{total} = \text{FSL}\,[\text{dB}] + L_m\,[\text{dB}] − G_t \,[\text{dB}] − G_r \,[\text{dB}]}.\end{equation}
where ##\text{FSL}## is the free space loss given by
\begin{equation}\text{FSL}\,[\text{dB}] = 20 \log\left|\frac{4πrf}{c_0}\frac{0.267+S}{0.2}\right|\end{equation}
and ##L_m## is the loss within the medium (undefined by Ghasemi.)
Depth of penetration
If we define depth of penetration as ##x\equiv1/\alpha##, where ##\alpha = \sqrt{\pi\mu\sigma f}## is the attenuation, so
\begin{equation}\begin{split}x&=\frac{1}{\sqrt{\pi\mu\sigma f}}\\&=\frac{1}{\sqrt{\pi\mu_0}}\cdot\frac{1}{\sqrt{\mu_r\sigma f}}\\&=892.0621\frac{1}{\sqrt{\mu_r\sigma f}}.\end{split}\end{equation}
Now, "for all practical purposes the relative permeability of salt water is 1," (Herring, 2007) so:
\begin{equation}\boxed{x=892.0621\frac{1}{\sqrt{\sigma f}}}.\end{equation}
The above is a simulation (using Excel) of the model, showing the penetration depth and absolute transmission loss as a function of frequency. Here we witness the penetration depth holding true to our expectations—if perhaps a little more extreme than expected—and the transmission loss showing the *opposite* of what the penetration depth shows.
Zoksimovski (2012) semi-empirical model
I did find a good experimental report, Underwater Electromagnetic Communications Using
Conduction – Channel Characterization (Zoksimovski et. al., 2012), which detailed three separate approximate models for radio wave attenuation using a channel transfer function ##H##, outlining two far-field approximations:
\begin{equation}|H| = A_0 e^{-\alpha_1\sqrt{f}} \ \ \ \ \ \ \ (1)\end{equation}
\begin{equation}|H| = A_0 e^{-\alpha_2 f} \ \ \ \ \ \ \ \ \ (2)\end{equation}
and a near-field approximation:
\begin{equation} \boxed{|H| = \frac{p_1f^2 + p_2f + p_3}{q_1f^2 + q_2f + q_3}\,e^{-\alpha_3 f}}.\end{equation}
I'm interested more-so in the near field due to the high observed attenuation of radio waves in seawater. The data provided by Zoksimovski et. al. was unclear at best, but averages were found to be ##p_1 = 0.75\times 10^{-5}##, ##p_2 = 2.30\times 10^{-4}##, ##p_3 = 17.25\times 10^{-5}##, ##q_1 = 0.30##, ##q_2 = 0.15##, ##q_3 = 0.18##, ##\alpha_3 = 0.55##. These were the values used in the following simulation.
As you can see this model produces *tiny* received signals which are killed off within 10 Hz. I know this to not be physically accurate. It also does not factor the distance between antenna anywhere into calculations.
This is the graphs produced by Zoksimovski et. al. which do not show the same trends as my simulation (see the thick blue lines for the model discussed.) Perhaps this is an error in my simulation, however intuition suggests that the low values of the parameters will influence the trend in the way I've simulated.
Cole-Cole Relation
The Cole-Cole relation—and its specialisation, the Debye relaxation model—was brought to my attention by O'Shaugnessy's 2012 brilliant paper, Characterising the Relative Permittivity and Conductivity of Seawater for Electromagnetic Communications in the Radio Band.
The Cole-Cole relation states that
\begin{equation} \hat{\epsilon}(\omega) = \epsilon_\infty + \frac{\Delta\epsilon}{1+(j\omega\tau)^{1-\alpha}} \end{equation}
where ##\hat{\epsilon}(\omega)## is the complex permittivity, ##\hat{\epsilon}(\omega) = \epsilon' + j\epsilon''##; ##\Delta\epsilon = \epsilon_s- \epsilon_\infty##, where ##\epsilon_s## is the static permittivity and ##\epsilon_\infty## is the infinite frequency permittivity; ##\omega = 2\pi f##; ##\tau## is the dielectric relaxation time; ##j = \sqrt{-1}##; and ##\alpha## is used to describe the spectral shape:
##\alpha = 0##, Debye model,
##\alpha > 0##, 'stretched' relaxation.
In turn,##\alpha > 0##, 'stretched' relaxation.
\begin{equation} \epsilon_r = \epsilon_\infty + \frac{\Delta\epsilon}{1 + j\frac{\omega\epsilon}{\sigma}} - j\frac{\sigma}{\omega\epsilon_0}, \end{equation}
where ##\sigma## is the conductivity of the medium.
I'll be honest, I don't fully understand this model, but I appreciate that it attempts to address the dependence of the relative permittivity on frequency. This seems like an important point.
Could anyone perhaps explain this model? How could this be applied into a model for radio propagation? Also, I'm still finding difficulty understanding the application of complex numbers in electromagnetism (such as in wave phase): how does it translate into real terms? It also appears in the following propagation model.
O'Shaugnessy's (2012) Dielectric Propagation Model
Again, this model is from Characterising the Relative Permittivity and Conductivity of Seawater for Electromagnetic Communications in the Radio Band (O'Shaugnessy's, 2012). It states that:
\begin{equation}\boxed{E_z = E_{0, z} e^{j\omega t - \gamma z}} \ \ \ \ ,\ \ \ \ \boxed{H_z = H_{0, z} e^{j\omega t - \gamma z}} \end{equation}
where ##E## represents the electric field strength, ##H## the magnetic field strength and
\begin{equation} \gamma_{\text{water}}=\alpha + j\beta = j\omega\sqrt{\mu\left( \epsilon - j \frac{\sigma}{\omega}. \right)} \end{equation}
The author then continues to discuss the conduction and dielectric bands of this model depending on the relationship between ##\frac{\sigma}{\omega}## and ##\epsilon##.
Could anyone help to explain this?
Last edited by a moderator: