Monkey_Man08
- 3
- 1
1. The problem statement: In the figure four particles form a square with edge length a = 2.44 × 10-2 m. The charges are q1 = q4 = 1.06 × 10-15 C and q2 = q3 = q. What is q if the net electrostatic force on particle 1 is zero?
All variables and given/known data: The given variable are in the statement, but I have calculated and checked some other important variables.
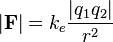 , where k = 8.99E9[/B]
, where k = 8.99E9[/B]
Since I'm using the above equation to solve for q2, I used algebra to set it up as q2 = (F)(r2) / (k)(q1). Once I plugged the numbers I have (6.00E-18)(1.19E-3) / (8.99E9)(1.06E-15). Once I plug all that in the calculator, I'm left with 7.49E-16 C. But supposedly that is the wrong answer. I've checked my math enough to know all the information above "The attempt at a solution" portion is correct, so the problem must lie within this final step... I think.
All variables and given/known data: The given variable are in the statement, but I have calculated and checked some other important variables.
- Net force acting on particle 1 by particle 4 is 8.45E-18 N.
- The X component of the force acting on particle 1 by particle 2 is negative 6.00E-18 N.
- Distance from particle 1 to particle 4 is 0.034507 m.
Homework Equations
: Coulomb Force:The Attempt at a Solution
Since I'm using the above equation to solve for q2, I used algebra to set it up as q2 = (F)(r2) / (k)(q1). Once I plugged the numbers I have (6.00E-18)(1.19E-3) / (8.99E9)(1.06E-15). Once I plug all that in the calculator, I'm left with 7.49E-16 C. But supposedly that is the wrong answer. I've checked my math enough to know all the information above "The attempt at a solution" portion is correct, so the problem must lie within this final step... I think.
