Saitama
- 4,244
- 93
I like Serena said:Try:
(ei(ϕ + 2kπ))3 = 1
But i am still getting -2kπ.
The value of n in the identity sin^3x sin 3x = ∑^n_{m=0} C_m cos mx is determined through the expansion of the left-hand side using trigonometric identities. The discussion reveals that the correct interpretation of the binomial coefficient C_m is crucial, as it relates to the powers of cosine in the expansion. The final expression indicates that n must equal 3, as the highest cosine term present is cos 3x.
PREREQUISITESMathematics students, educators, and anyone interested in advanced trigonometric identities and their applications in calculus and algebra.
I like Serena said:Try:
(ei(ϕ + 2kπ))3 = 1
I like Serena said:Look at it this way:
You already had:
ei(3ϕ) = 1
So:
cos(3ϕ) + i sin(3ϕ) = 1
This means that
cos(3ϕ) = 1 and sin(3ϕ) = 0
Can you solve that?
Pranav-Arora said:ϕ=0.
Pranav-Arora said:I want to know why you take z=eiϕ?
I like Serena said:Err... no.
The solution of cos(3ϕ) = 1
is 3ϕ=0 mod 2π,
which comes out as ϕ = 0 mod (2/3)π.
My bad, I thought you already knew this.
But now that I think about it, I recall that you did not know the "mod" notation yet.
So are you aware of the periodicity of the cosine function?
That is has a period 2π?
I like Serena said:Actually, I didn't do that quite right.
It should be:
z = r eiϕ
Any complex number z has 2 representations:
z = x + i y
z = r eiϕ
Are you aware of the first representation?
The second form follows from the first combined with Euler's formula.
Pranav-Arora said:Yes, i know about the periodicity of cosine function which is 2π.
Pranav-Arora said:I know about the first representation.
But i don't know about the second one.
Yep, i found out three solutions using graph.I like Serena said:So do you get that cos(3ϕ) = 1 has 3 solutions?
I like Serena said:Are you familiar with so called polar coordinates?
That is:
x = r cos(ϕ)
y = r sin(ϕ)
Pranav-Arora said:No, i don't know about polar coordinates.
Pranav-Arora said:Yep, i found out three solutions using graph.
Is there any other way to find the number of solutions?
I like Serena said:Well, I guess we're chunking off a bit more than I originally thought.
But then, you seem so knowledgeable already!
Well, as long as you want to learn, that's fine by me.
Here's a picture that shows which r and phi I'm talking about (in the picture they use theta instead of phi though).
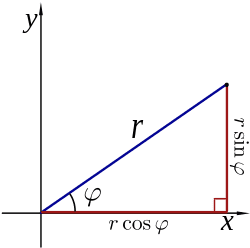
If you have a point (x, y) it has a distance to the origin, which we call "r".
As you can see in the picture, you can define a rectangular triangle with an angle.
If you apply the definition of the cosine and the sine, you should be able to see that
x = r cos angle
y = r sin angle
That's it!
This is what we call polar coordinates, which is a different way to identify points in a plane.
I like Serena said:Erm... what are you thinking of?
The key is that any angle has a period of 2pi.
Pranav-Arora said:Thank you for your explanation I Like Serena!
So now let's get back to the question i.e. z=reiϕ.
Pranav-Arora said:To find the solutions of cos3x=1, what i did was that i draw a graph of cos 3x, then draw a line parallel to x-axis at y=1 on the graph of cos 3x. The points where both the graphs intersect are the solutions for cos 3x=1.
This method is graphical but i want to know the other way to find the number of solutions for cos3x=1, i don't want to use graphical method.
Substituting Euler's formula:-I like Serena said:What do you get if you substitute Euler's formula?
I like Serena said:Well, the algebraic method is to use the "mod 2pi" notation, or the "+2 k pi" notation, meaning that a cosine will be the same if you use an angle that is a multiple of 2pi bigger or smaller.
And another graphical method, is to look at the polar coordinates and consider what the angle should be to come out at (1, 0).
What do you know already of this?
Pranav-Arora said:Substituting Euler's formula:-
z=r(cosx+isinx)
What's this "r"?
Pranav-Arora said:I think i should not go to algebraic method.
I like Serena said:The same r as in the polar coordinates.
It is the distance of point (X, Y) to the origin, where z = X + i Y.
Btw, I used capital letters to distinguish them from the "x" in your equation which is actually phi.
Taking it one step further, you have:
z = r cosx + i r sinx = X + i Y
Do you see now?
I like Serena said:Nice icon!
So you have not learned yet how to solve cos x = c?
Pranav-Arora said:Got it now! I would print this disccussion to keep it for my reference.
So what should be the answer of z3=1?
I like Serena said:In exponential notation:
z1 = 1
z2 = ei(2/3)π
z3 = ei(4/3)π
In cartesian notation:
z1 = 1
z2 = -½ + i ½√3
z3 = -½ - i ½√3
Pranav-Arora said:How did you get
z2 = ei(2/3)π
z3 = ei(4/3)π

I like Serena said:What do you get if you substitute them in the equation z3 = 1?
Pranav-Arora said:Substituting z2, ei2n=1
Substituting z3, ei4n=1
Solving both the equations i get n=0.
But how do you get the solutions?
I like Serena said:Ah, I see, there is some confusion about π.
That might explain some of the confusion in the previous posts.
Well, π is π and not n.
See the difference?
It's a bit of a font problem I'm afraid.

Pranav-Arora said:Okay i again substitute the values,
Substituting z2, ei2\pi=1
Substituting z3, ei4\pi=1
How do you get these solutions?
I like Serena said:First you will need to understand why these are solutions.
Can you use Euler's formula to convert them to cosine/sine form?
Pranav-Arora said:Applying Euler's formula:-
ei2\pi=1
\Rightarrowcos2\pi+isin\pi=1
\Rightarrowcos2\pi+isin\pi=1
I like Serena said:Erm... you did not substitute correctly.
And then, do you understand why this is a solution?
What is cos(2pi)?
Pranav-Arora said:Oops sorry, it should be sin 2pi.
I think this is the solution because if we further solve the sine and cosine we get 1 which is equal to the right hand side of the equation.
cos(2pi) is 1.
I like Serena said:Exactly!
What about the other solution?
What is cos(4pi)? And sin(4pi)?
Do you perhaps understand now how to I found these solutions?
Pranav-Arora said:cos(4pi) is 1 and sin(4pi) is 0, but i still don't understand how you find out the solution?