tomrja
- 18
- 0
Homework Statement
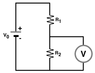
The output of the voltage-divider network shown in the diagram below is to be measured with two different voltmeters, V1 and V2. Consider the situation when V0 = 32.4 V, R1 = 205 Ω, and R2 = 465 Ω.
a) When the voltmeter V1, whose internal resistance is 4.80 k Ω is placed across R2, what would be the reading on the voltmeter V1?
b) When the voltmeter V2, whose internal resistance is 2.75 M Ω, is placed across R2, what would be the reading on the voltmeter V2?
Homework Equations
1/Req=(1/R1)+(1/R2) where Req= equivalent resistance
Req=R1+R2
V=IR
The Attempt at a Solution
I really do not know where to start with this problem. I originally found the equivalent resistance using the resistors in parallel equation and used that resistance to calculate the voltage that was running through that resistor. Using Kirchoff's Rule that the equation for the circuit was V-R1*I-Req*I=0 where Req in this case is the equivalent resistance of the voltmeter and R2. I guess am having trouble understanding what the voltmeter actually does to the circuit.