What is the weight that will balance the object Q?

[Kile]

Here is diagram for Tower Crane.

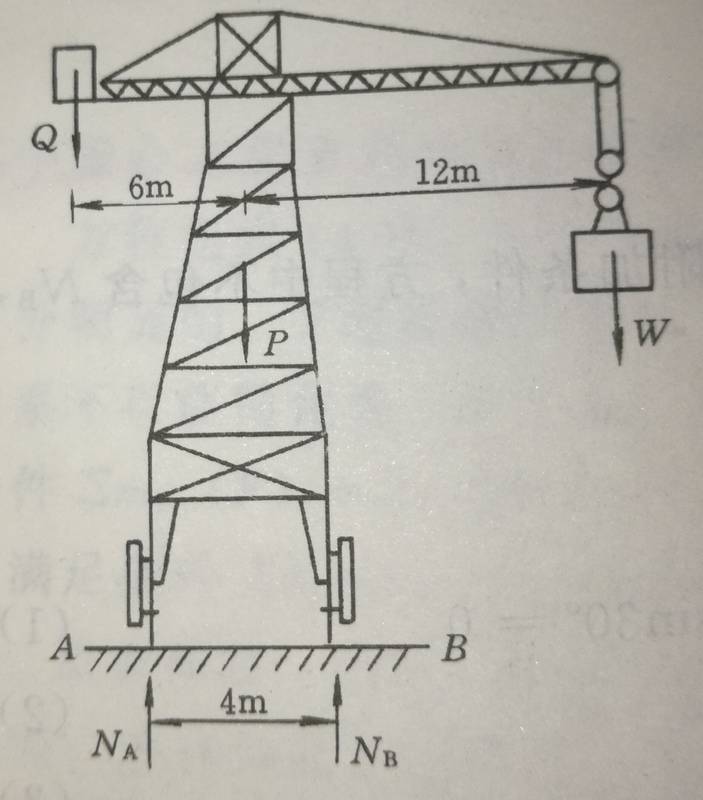
The Rack weight P=700kN, and the maximum load capacity for this crane is W=200kN. The long beam length is 12 metres, and the balance object weighs Q. The short beam length is 6 metres. What is the weight of Q to keep the crane's balance at all situation?

 

[Kile]

Why should it be like that?
There are 2 situations
Full load, W=200 kN. let $Q_{min}$ stands for the minimum weight requirement of Q.

$$\sum m_B(F)=0, (6+2)Q_{min} + 2P - (12-2) W=0, N_A=0$$

No load, W=0 kN. let $Q_{max}$ stands for the maximum weight requirement of Q

$$\sum m_A(F)=0, (6-2)Q_{max} - 2P =0, N_B=0$$