What is wrong with my summation formula?

[DerekZ10]

Im trying to find a general formula I can store in my calculator that can find the number of onto (surjective) functions exists for a relation of when M is mapped to N.

I can't seem to find a nice formula for it, but based on the below material I will show you what I have developed.

From: Discrete Mathemeatics and Its Applications 7th Edition Rosen pg. 561

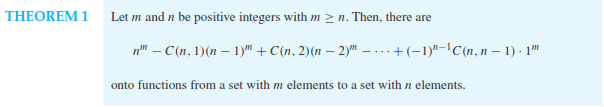From: Discrete Mathemeatics and Its Applications 7th Edition Rosen pg. 512

Random Chegg Problem from Google Search I'm using to verify with:

Here is what I've formed, written out:

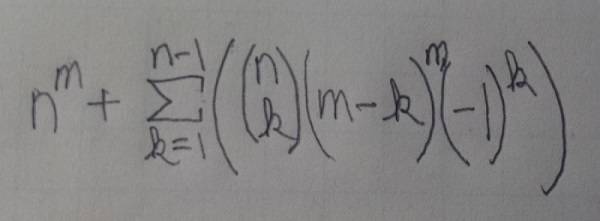
In the TI nSpire CX CAS, it's written like this:

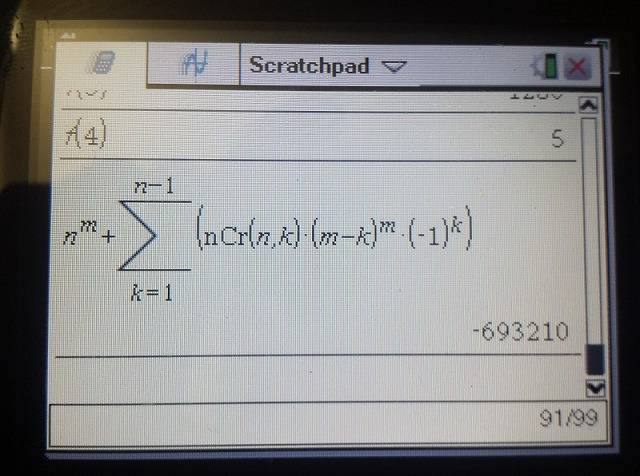
And as you can see, the chegg problem I'm trying to verify it with doesn't match!
But I think it should! If I manually iterate the function like so:

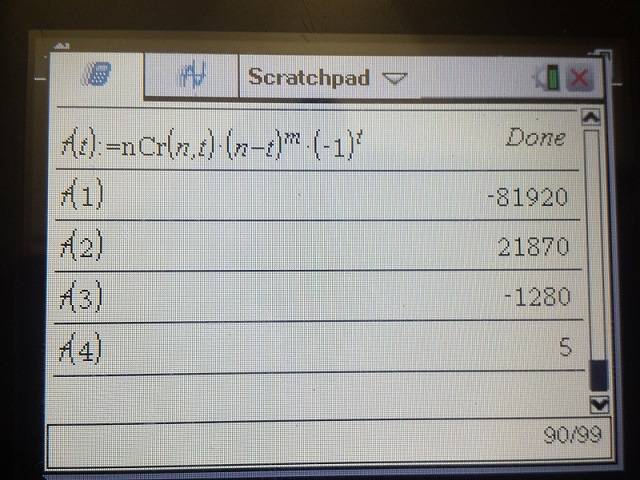The values are correct and what Chegg is showing. What have I done wrong in my equation?

 

[gopher_p]

Did you check that your summation formula matches the version that doesn't use sigma notation? i.e are all your $m$s and $n$s where they're supposed to be?

 

[DerekZ10]

Wow, good call! I don't know how I constantly was missing that the (m-k) portion that should have been (n-k). And I even had it right in the non iterative equation.