Circular antenna array formula

[Unconscious]

At page 20 of this pdf the two formulas that characterize the behavior of a linear and a circular antenna array are compared.
The reason why I write this post is: I don't understand why the second formula is true.
Below I show why I am not convinced.

In general, given a configuration of sources (currents impressed) in the vacuum we can write that the vector potential is equal to:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\underbrace{\int_V \mathbf{J}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V}_{\mathcal{a}(\theta,\phi)}$

where (as usual) $k=\frac{2\pi f}{c}$ ($f$ frequency and $c$ speed of light), $\mathbf{r}_0$ unit vector pointing at the field evaluation point (at a distance $r$ from the origin) and $\mathbf{r}'$ source point.
We detail this expression for a discrete circular configuration on the xy plane, where the points drawed are the 'centers' of the current distribution of every element in the array:

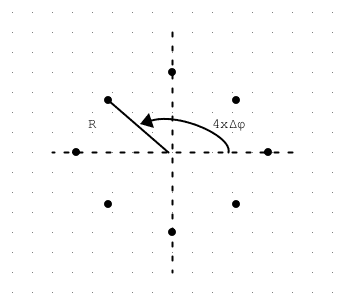
and we use the cylindrical coordinates for $\mathbf{r}'$:

$\mathcal{a}(\theta,\phi)=\int_V \mathbf{J}(r',\phi',z')e^{jk\left (r'\sin\theta\cos (\phi-\phi')+z'\cos\theta \right )}r'\mathrm{d}r'\mathrm{d}\phi'\mathrm{d}z'$

which can be written equivalently as:

$\mathcal{a}(\theta,\phi)=\sum_n\int_{V_n} \mathbf{J}^{(n)}(r',\phi',z')e^{jk\left (r'\sin\theta\cos (\phi-\phi')+z'\cos\theta \right )}r'\mathrm{d}r'\mathrm{d}\phi'\mathrm{d}z'$

Then, using the property $\mathbf{J}^{(n)}(r',\phi',z') = a_n \mathbf{J}^{(0)}(r',\phi'-n\Delta\phi,z')$ ($a_n$ complex number) and taking advantage of the simple change of coordinates $\widetilde{\phi}=\phi'-n\Delta\phi$ we arrive at:

$\mathcal{a}(\theta,\phi)=\sum_n a_n \int_{V_0} \mathbf{J}^{(0)}(r',\widetilde{\phi},z')e^{jk\left (r'\sin\theta\cos (\phi-\widetilde{\phi}-n\Delta\phi)+z'\cos\theta \right )}r'\mathrm{d}r'\mathrm{d}\widetilde{\phi}\mathrm{d}z'$

The latter formula, if calculated at observation points 'on the ground' ($\theta = \pi / 2$, which is the hypothesis in which the book is put to come up with its formula (2.2) on page 20) is reduced to:

$\mathcal{a}(\phi)=\sum_n a_n \underbrace{\int_{V_0} \mathbf{J}^{(0)}(r',\widetilde{\phi},z')e^{jk\left (r'\cos (\phi-\widetilde{\phi}-n\Delta\phi) \right )}r'\mathrm{d}r'\mathrm{d}\widetilde{\phi}\mathrm{d}z'}_{\text{EL}(\phi-n\Delta\phi)}$

in which the 'element factor' $\text {EL} (\phi-n \Delta \phi)$ has been written in compact form, that is the radiation integral of the single element of the array.
You can clearly see the difference with respect to formula (2.2) on the page cited above: a complex exponential factor is missing in the summation.

Where does it have to come from, and where am I wrong?

 

[marcusl]

I think you neglected to include the element factor in your initial expression for the vector potential. The element factor is a weighting term that shows how much field is radiated in a direction r for the current at r' so, as written, you are specifying an omni-directional element (which, of course, exists for an acoustic source but not for an EM source in 3D). I also think that you need to include a delta function starting in your second integral to specify positions of the discrete antenna elements in the array. The exponential in what you identified as the element pattern in your last equation is, in fact, the exponential of (2.11) that you are asking about.

 

[Unconscious]

I think you neglected to include the element factor in your initial expression for the vector potential.

No, the element factor has to come up naturally from my first formula, just as it actually did, as you can see from the last formula I wrote.

as written, you are specifying an omni-directional element

It is not so, in my first expression there is $\mathbf{J}(\mathbf{r}')$, the whole $\mathbf{J}(\mathbf{r}')$, which contains everything, it is not the case of omnidirectional elements.

I also think that you need to include a delta function starting in your second integral to specify positions of the discrete antenna elements in the array.

The delta are not needed because the elements are not point-like. The dots you see drawn are just the 'centers' (an arbitrary point chosen as a reference) of the current distributions.

The exponential in what you identified as the element pattern in your last equation is, in fact, the exponential of (2.11) that you are asking about.

No, my exponential has the integration variables in the exponent and it schematizes the fact that the various element factors must be calculated in different azimuthal angles of view, as it should be seen from the fact that the elements are rotated and not rigidly translated between them. Its exponential is still another, different from mine (as you can see, in its formula there is the radius of the circle on which the elements are arranged).

 

[marcusl]

Your "element factor" isn't--terms describing the offset of each antenna from the origin ($n\Delta\phi$, e.g.) belong in the array factor. Back up to your first equation, writing it for a single element

$\mathbf{A}^{(n)}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\int_{V'} \mathbf{J}^{(n)}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V'$,

and build up your array by adding together elements that are offset from the origin

$\mathbf{A}(\mathbf{r})=\sum_n\mathbf{A}^{(n)}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n\int_{V'} \mathbf{J}^{(n)}(r',\phi',z')e^{jk\mathbf{r}_0\cdot (\mathbf{r}'-\Delta\mathbf{r}_n)}\mathrm{d}V'$.

Finally, break the exponential into the product of two terms

$\mathbf{A}^{(n)}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_ne^{-jk\mathbf{r}_0\cdot \Delta\mathbf{r}_n}\int_{V'} \mathbf{J}^{(n)}(r',\phi',z')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V'$.

The integral is the element factor of the n^th element. Now you can convert to cylindrical coordinates.
EDIT:
This expression is general for any array and any geometry.

For reference, we can examine the special case of identical antenna elements (although it is not the geometry of interest in the original post). In the event that the antenna elements are identical and have identical orientations, differing only by a constant excitation scale factor $a_n$, then we can replace $\mathbf{J}^{(n)}$ with $a_n\mathbf{J}^{(0)}$. Since this $\mathbf{J}^{(0)}$ term is the same for all n, we can factor it out in front of the summation.

$\mathbf{A}^{(n)}(\mathbf{r})=\left[\frac{e^{-jkr}}{4\pi r}\int_{V'} \mathbf{J}^{(0)}(r',\phi',z')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V'\right]\left[\sum_na_ne^{-jk\mathbf{r}_0\cdot \Delta\mathbf{r}_n}\right]=(EF)(AF)$.

This element factor (EF) multiplies the term in the summation, called the array factor (AF). It's clear, now, why the two terms are called "factors."

 

[Unconscious]

$\mathbf{A}(\mathbf{r})=\sum_n\mathbf{A}^{(n)}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n\int_{V'} \mathbf{J}^{(n)}(r',\phi',z')e^{jk\mathbf{r}_0\cdot (\mathbf{r}'-\Delta\mathbf{r}_n)}\mathrm{d}V'$.

It is precisely this formula that cannot be applied to my case, because when you write $(\mathbf{r}'-\Delta\mathbf{r}_n)$ you are actually schematizing a generic array where, however, the elements are obtained using only and solely rigid translations of a reference element: this is not the situation in which the book is placed (linked pdf). When we talk about circular arrays we are not referring to arrays in which the elements are simply all oriented in the same way, albeit arranged on a circle, but we are meaning an even stronger thing, that is, they are also rotated.

In pictures, your formula (applied to a circular layout) says that:

which is different from that:

that is our situation.
This is also confirmed by the fact that for these types of arrays the 'array factor' does not exist, because the classic formula you wrote at the end of your post with the multiplication between element factor and array factor does not exist at all. For further confirmation of this, read the final sentence on page 20:

The element function can, therefore, in general not be brought outside the summation, since it is a function of the element position; there is no common element factor.

 

[marcusl]

Please know that I am unable to open your link so I am just responding to what is in your posts--I cannot see what your textbook says. My equation

$\mathbf{A}^{(n)}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\int_{V'} \mathbf{J}^{(n)}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V'$

contains no assumptions about the orientations of the antennas. If the antennas are horns, for example, then $\mathbf{J}^{(n)}$ represents the collection of current densities on the metallic walls of the n^th horn. To model the first 8-element array pictured above, all $\mathbf{J}$ are identical. To model the second array, the currents $\mathbf{J}^{(3)}$ are rotated by 90 degrees compared to the currents $\mathbf{J}^{(1)}$ for the horn on the x-axis. Vector $\Delta\mathbf{r}_n$ refers to the displacement away from the array origin of a common reference point on each antenna--the horn's phase center, for example--and does not perform any rotation, as you note. Rotations are contained within the $\mathbf{J}$.

I included the last comment in post #4, involving identical elements, for the benefit of those who may read this thread without knowledge of specialized phased array terms. The factorization explains why the two terms are called element factor and array factor. Arrays whose element factor may be brought outside of the summation are said to have radiation patterns characterized by pattern multiplication.

 

[marcusl]

Just to follow up on an additional point: you are correct that an array factor does not exist for a circular array of antennas with non-identical element patterns. I have edited my previous post to clarify the wording.

 

[Unconscious]

Please know that I am unable to open your link so I am just responding to what is in your posts--I cannot see what your textbook says.

The linked pdf is an extract of the second chapter of the book 'Conformal array antenna theory and design' of IEEE Press.

My equation

$\mathbf{A}^{(n)}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\int_{V'} \mathbf{J}^{(n)}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V'$

contains no assumptions about the orientations of the antennas. If the antennas are horns, for example, then $\mathbf{J}^{(n)}$ represents the collection of current densities on the metallic walls of the n^th horn.

Yes, it's true, in fact I said that this other equation is not applicable to our case:

$\mathbf{A}(\mathbf{r})=\sum_n\mathbf{A}^{(n)}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n\int_{V'} \mathbf{J}^{(n)}(r',\phi',z')e^{jk\mathbf{r}_0\cdot (\mathbf{r}'-\Delta\mathbf{r}_n)}\mathrm{d}V'$

because $(\mathbf{r}'-\Delta\mathbf{r}_n)$ is a rigid traslation of the current source distribution of one reference element (in the picture I omit the simbol $\Delta$):

To model the first 8-element array pictured above, all $\mathbf{J}$ are identical. To model the second array, the currents $\mathbf{J}^{(3)}$ are rotated by 90 degrees compared to the currents $\mathbf{J}^{(1)}$ for the horn on the x-axis.

Exactly.

Vector $\Delta\mathbf{r}_n$ refers to the displacement away from the array origin of a common reference point on each antenna--the horn's phase center, for example--and does not perform any rotation, as you note. Rotations are contained within the $\mathbf{J}$.

I don't agree with this point, that is the core of my problem.
$\mathbf{r}'$ is the integration variable (three variables $x',y',z'$ or $r',\phi',z'$, and so on...). In my picture above the vector $\mathbf{r}'$ 'sweeps' all the sources distribution:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\int_{V'} \mathbf{J}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V'$

then we have to split the whole single integral into a sum of n integrals:

that matematically we have to write in this way:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n \int_{V_n'} \mathbf{J}^{(n)}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V_n'$

Then, we use the fact that every source distribution in every $V_n'$ is simply a rigid translation of the source distirbution in $V_1'$: $\mathbf{J}^{(n)}(\mathbf{r}') = a_n \mathbf{J}^{(1)}(\mathbf{r}'-\Delta\mathbf{r}_n)$. The formula appears then in this way:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n a_n\int_{V_n'} \mathbf{J}^{(1)}(\mathbf{r}'-\Delta\mathbf{r}_n)e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V_n'$

At this point we make a change of variables $\widetilde{\mathbf{r}}=(\mathbf{r}'-\Delta\mathbf{r}_n)$:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n a_n\int_{V_1'} \mathbf{J}^{(1)}(\widetilde{\mathbf{r}})e^{jk\mathbf{r}_0\cdot (\widetilde{\mathbf{r}}+\Delta\mathbf{r}_n)}\mathrm{d}\widetilde{\mathbf{r}}$

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n a_n e^{jk\mathbf{r}_0\cdot \Delta\mathbf{r}_n} \int_{V_1'} \mathbf{J}^{(1)}(\widetilde{\mathbf{r}})e^{jk\mathbf{r}_0\cdot \widetilde{\mathbf{r}}}\mathrm{d}\widetilde{\mathbf{r}}$

If you agree with all this mathematical steps, then for a circular array (in which the elements are also rotated):

tha math is the same until here:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n \int_{V_n'} \mathbf{J}^{(n)}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V_n'$

but then we cannot say:

Then, we use the fact that every source distribution in every $V_n'$ is simply a rigid translation of the source distirbution in $V_1'$: $\mathbf{J}^{(n)}(\mathbf{r}') = a_n \mathbf{J}^{(1)}(\mathbf{r}'-\Delta\mathbf{r}_n)$. The formula appears then in this way:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n a_n\int_{V_n'} \mathbf{J}^{(1)}(\mathbf{r}'-\Delta\mathbf{r}_n)e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V_n'$

but we have to say that $\mathbf{J}^{(n)}(\mathbf{r}'=(r',\phi',z')) = a_n \mathbf{J}^{(1)}((r',\phi'-n\Delta\phi,z'))$.

Do you agree until here?

 

[marcusl]

I don't really follow your logic, and it seems to get you into trouble. Try separating the effects of displacement, which refers to the position of the n^th antenna, from what is happening inside of the n^th antenna, which is where the rotation lies. The first imparts a phase shift onto the field from each antenna, as seen from the far field observation point, while the second affects how much field amplitude each antenna radiates towards that distant point. Thus, put your rotation into $\mathbf{J}^{(n)}$ and it should work out fine.

 

[hutchphd]

and build up your array by adding together elements that are offset from the origin

A(r)=∑nA(n)(r)=e−jkr4πr∑n∫V′J(n)(r′,ϕ′,z′)ejkr0⋅(r′−Δrn)dV′.

Finally, break the exponential into the product of two terms

units??
Please recheck your work using all the tools in your bag. What you are attempting seems correct to me but you need to take care.

Sorry I see r0 is a unit vector (don't like that notation...)

 

[Unconscious]

I don't really follow your logic.

Could I ask you where you see logic errors, please?
Is there a particular step in my analysis in the first/last message that is wrong?

 

[marcusl]

The first equation below is weird--why set up separate integrals over N different volumes? You'll have a hard time keeping track of things properly.

View attachment 274880

that matematically we have to write in this way:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n \int_{V_n'} \mathbf{J}^{(n)}(\mathbf{r}')e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V_n'$

Then, we use the fact that every source distribution in every $V_n'$ is simply a rigid translation of the source distirbution in $V_1'$: $\mathbf{J}^{(n)}(\mathbf{r}') = a_n \mathbf{J}^{(1)}(\mathbf{r}'-\Delta\mathbf{r}_n)$. The formula appears then in this way:

$\mathbf{A}(\mathbf{r})=\frac{e^{-jkr}}{4\pi r}\sum_n a_n\int_{V_n'} \mathbf{J}^{(1)}(\mathbf{r}'-\Delta\mathbf{r}_n)e^{jk\mathbf{r}_0\cdot \mathbf{r}'}\mathrm{d}V_n'$

I think the last equation is also wrong: you've changed integration variables to $\mathbf{t}_n=\mathbf{r}'-\Delta\mathbf{r}_n$ in the current density, so you have to change it elsewhere in the integral, including in the exponential.

 

[Unconscious]

The first equation below is weird--why set up separate integrals over N different volumes?

I set up the problem this way because I followed the path my antenna book taught me, but it only set the problem for arrays whose source distributions do not rotate (which would be like I did in post #8).

In the last equation there is no change of integration variables. There, it was only used the fact that the sources are 'similar', that is $\mathbf{J}^{(n)}(\mathbf{r}')=a_n\mathbf{J}^{(1)}(\mathbf{r}'-\Delta\mathbf{r}_n)$.
Tha change of integration variable happens successively.

I understand how you set the problem (you start writing $n$ different potentials $\mathbf{A}^{(n)}$), but I would like to understand why the other way I set it does not bring the same result (I start by thinking of the whole array as a single antenna, that is a single global $\mathbf{A}$ given by a single global $\mathbf{J }$, and then let the math tell me things), there is somewhere an error that I do not see, and unfortunately it is not among the ones you told me in the previous message (I think), for the reasons I have explained now.
In any case, I think that the confirmation that this method must also work lies in the fact that in the case of sources that do not rotate, but only rigidly translate between them, the development done in message #8 has led to the correct result.

 

[marcusl]

I have given you a correct calculation and also have tried to understand your approach. Since I have, you say, failed at that, I will move on. Perhaps someone else here can help you. I hope you find what you are looking for.

 

[Unconscious]

I had no intention of being rude, I was just exposing my thoughts trying to argue it as best as possible. I am sorry to have offended you.

Thank you for the time you have dedicated to me.

 

[marcusl]

No offense taken, I just don't seem to be helping. I do wish you luck in your quest.