What's the field strength and pattern rules for bar magnets attached?

Click For Summary
SUMMARY

The discussion focuses on the magnetic field strength and pattern rules for bar magnets when attached together. It concludes that when two bar magnets are joined with opposite poles (N/S), the resulting magnetic field is weaker than that of a single bar magnet. Specifically, the configuration where both magnets are aligned with the same poles (N/N or S/S) results in zero magnetic field due to the cancellation of induced currents. The answer to the posed problem is definitively D, not A, indicating a misunderstanding of the interaction between the magnets.

PREREQUISITES
  • Understanding of basic magnetism principles
  • Knowledge of magnetic field strength and patterns
  • Familiarity with bar magnet configurations
  • Concept of induced currents in magnetic fields
NEXT STEPS
  • Research the effects of magnetic field strength in different bar magnet configurations
  • Learn about the principles of magnetic field line patterns
  • Study the concept of induced currents in electromagnetism
  • Explore advanced topics in magnetism, such as magnetic field interactions
USEFUL FOR

Students of physics, educators teaching magnetism, and hobbyists experimenting with bar magnets will benefit from this discussion.

pkc111
Messages
224
Reaction score
26
TL;DR
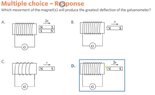
What are the field strength and pattern rules for bar magnets attached to each other?
The attached probem tricked me because the answer is apparently D and not A.
Presumably because the magnetic field is weaker with 2 bar magnets joined N/S compared to a single bar magnet.
So this seems to be a gap in my knowledge as to the resulting strengths of magnets joined together. Are there any rules. I assume the magnetic strength is not 0 for the magnets in A, so what % loss will there be? What will the field lines look like? What if they were tied the other way N/N and S/S?
Many thanks
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    28.2 KB · Views: 132
Physics news on Phys.org
pkc111 said:
Summary:: What are the field strength and pattern rules for bar magnets attached to each other?

What if they were tied the other way N/N and S/S?
Double current wrt D will be observed.

Zero current will be observed for A. Opposite induced currents by the opposite polar magnets cancel.
 
Last edited:

Similar threads

Undergrad Pushing a rod in a magnetic field
  • · Replies 15 ·
Replies
15
Views
3K
Non-Uniform Magnetic Field Calculations
  • · Replies 9 ·
Replies
9
Views
2K
Undergrad What Materials Can Shield Electronics from a 3-Tesla MRI Magnetic Field?
  • · Replies 12 ·
Replies
12
Views
2K
High School Experiment issues (electromagnetism)
  • · Replies 42 ·
2
Replies
42
Views
3K
Multipole ring magnet generator
  • · Replies 9 ·
Replies
9
Views
3K
Motional EMF in the presence of a time-varying magnetic field
  • · Replies 11 ·
Replies
11
Views
3K
Undergrad Parallel magnet B-field strength
  • · Replies 2 ·
Replies
2
Views
2K
Making sense of sequence of ideas in MIT OCW's 8.02 notes on Faraday
  • · Replies 1 ·
Replies
1
Views
2K
What is the induced magnetic force on this closed current loop?
  • · Replies 12 ·
Replies
12
Views
2K
Understanding work in translation and rotation of a magnetic dipole
  • · Replies 1 ·
Replies
1
Views
2K