What's the fundamental group of a punctured torus?

Click For Summary
SUMMARY

The fundamental group of a punctured torus is Z x Z, as established in the discussion. Initially, there was confusion regarding whether it could be represented as Z x Z x Z due to a misunderstanding of its topology. The correct interpretation involves recognizing that a punctured torus can be continuously deformed into two cylinders glued to a square patch, confirming that the fundamental group is indeed Z x Z. This clarification resolves the debate on the structure of the fundamental group for this geometric shape.

PREREQUISITES
  • Understanding of fundamental groups in algebraic topology
  • Familiarity with toroidal geometry
  • Knowledge of continuous deformation and homeomorphism concepts
  • Basic grasp of group theory, specifically free groups
NEXT STEPS
  • Study the properties of fundamental groups in algebraic topology
  • Explore the concept of homotopy and its relation to punctured surfaces
  • Learn about the classification of surfaces and their fundamental groups
  • Investigate the implications of the Seifert-van Kampen theorem in topology
USEFUL FOR

Mathematicians, particularly those specializing in topology, geometry students, and anyone interested in the algebraic properties of surfaces and their fundamental groups.

kakarotyjn
Messages
95
Reaction score
0
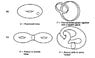
The fundamental group of a torus is Z*Z,then the fundamental group of a punctured torus is Z*Z*Z.

But I've ever done a problem,it said a punctured torus can be continuously deformed into two cylinders glued to a square patch.Really?

If that is right,then the fundamental group of punctured torus is Z*Z.

Which is right?Need help:smile:
 

Attachments

  • http_imgload.jpg
    http_imgload.jpg
    21.7 KB · Views: 2,364
Physics news on Phys.org
Yes, it's true... imagine making the hole bigger and bigger.. make it as big as you can withouth changing the topology. You're left with the two strips glued on a square patch.
 
oh,i see.the fundamental group should be Z*Z. i consider an extra loop,which is the edge circle of the punctured hole. but now I know it's the 2 power of a generator.
 
The fundamental group of the torus is not Z*Z though, it is ZxZ.
 

Similar threads

Graduate Fundamental Group of the Torus-Figure 8
  • · Replies 3 ·
Replies
3
Views
5K
Graduate Why Is the Fundamental Group of a Torus Described as Z+Z Instead of ZxZ?
  • · Replies 3 ·
Replies
3
Views
3K
Graduate About Chern number of U(1) principal bundle on a torus
  • · Replies 28 ·
Replies
28
Views
7K
Graduate ± sqrt(b^2 - a^2) = ± b ± ai ?
  • · Replies 6 ·
Replies
6
Views
3K
Graduate Fundamental group of n connect tori with one point removed
  • · Replies 9 ·
Replies
9
Views
4K
Graduate Can I find a smooth vector field on the patches of a torus?
  • · Replies 4 ·
Replies
4
Views
3K
Graduate What is the connection between the mapping class group of a torus and Gl(2,Z)?
  • · Replies 2 ·
Replies
2
Views
4K
Graduate Classification of reductive groups via root datum
  • · Replies 3 ·
Replies
3
Views
3K
Graduate Fundamental group of Project Plane with 2 points missing
  • · Replies 6 ·
Replies
6
Views
4K
Undergrad Fundamental theorem of arithmetic from Jordan-Hölder theorem
  • · Replies 5 ·
Replies
5
Views
3K