Can I find a smooth vector field on the patches of a torus?

[lichen1983312]

I am looks at problems that use the line integrals $\frac{i}{{2\pi }}\oint_C A$ over a closed loop to evaluate the Chern number $\frac{i}{{2\pi }}\int_T F$ of a U(1) bundle on a torus . I am looking at two literatures, in the first one the torus is divided like this

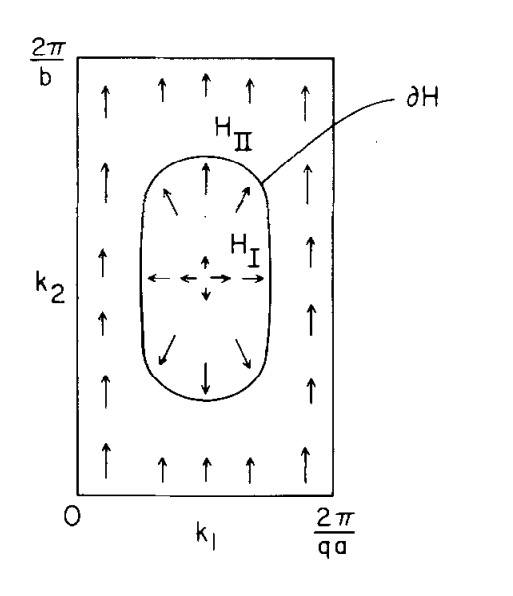
then the Chern number is computed as the difference $\frac{i}{{2\pi }}\left( {\oint_C {{A^I}} - \oint_C {{A^{II}}} } \right)$, this can be done because a smooth $A$ on both patches can be defined, since both patch I and II are contractible.

However, I am also looking at another litherature, the patches are divided as

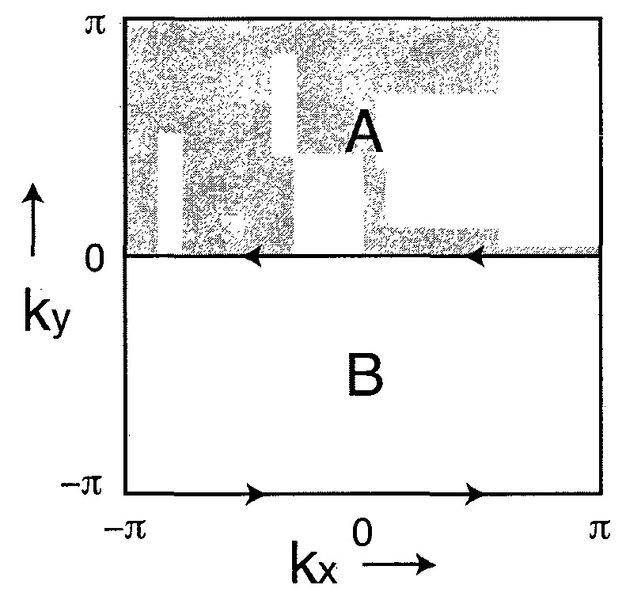
The author says although the two patches A and B are not contractible, a smooth vector bundle over A and B can still be found:

and the Chern number is evaluated in the same manner as the first case. I cannot find out why a smooth vector bundle on A or B must exist, can anybody explain ?
thanks very much .

 

[lavinia]

It seems that in the first picture you are integrating the Chern form over a disk shaped region $H_{1}$ and the rest of the torus minus $H_{1}$. $H_{1}$ is contractible but its complement $H_{2}$ is not. $H_{2}$ deforms continuously onto a figure 8 , not onto a point.

In the second picture it looks like you are cutting the torus into two cylinders. A cylinder is not contractible. It deforms continuously onto a circle.

These deformations show that the second real homology group of each of the pieces $H_{1,2}$, and the two cylinders $A$ and $B$ is zero. From De Rham's Theorem (for smooth manifolds with boundary), the Chern form is exact on each of them. In your notation, for each region $R$ there is a 1 form $A_{R}$ such that $dA_{R} = F$ on $R$.

This proof did not require showing that the bundle is trivial over each region.

- For any smooth n-plane bundle over a compact n-dimensional manifold, there is a smooth section that is zero except for a finite number of isolated zeros. These zeros can be chosen to lie in any open subset of the manifold. So if one chooses all of the zeros to lie in for instance $H_{1}$ then the section is non-zero on $H_{2}$. If the zeros are chosen to lie in $A$ then the section is non-zero over $B$. In the case of a complex line bundle over a surface e.g. the torus, there is a second linearly independent section with the same zeros.

- The argument that the bundle is trivial over $H_{1}$ because $H_{1}$ is contractible has a generalization that applies to other regions that are not contractible. The theorem is that if $f:X→Y$ is a homotopy equivalence between paracompact topological spaces, then every bundle over $X$ is an induced bundle $f^{*}(V)$of a bundle over $Y$. The projection map, $p$ of the cylinder $A$ or $B$ onto one of its boundary circles is a homotopy equivalence. Every bundle over the cylinder is an induced bundle $p^{*}(V)$of a bundle $V$ over the circle. Since the only oriented $U(1)$ bundle over the circle is trivial, it follows easily that an oriented $U(1)$ bundle over the cylinder is also trivial. For $H_{1}$ the projection onto any of its points is a homotopy equivalence so every bundle is induced from a bundle over a point. The projection of $H_{2}$ onto a figure 8 is a homotopy equivalence as well. Not sure about the vector bundles on a figure 8 . A reference for the theorem on homotopy equivalence is Hatcher, Vector Bundles and K-Theory. See Corollary 1.8 on page 21.

 

[lichen1983312]

It seems that in the first picture you are integrating the Chern form over a disk shaped region $H_{1}$ and the rest of the torus minus $H_{1}$. $H_{1}$ is contractible but its complement $H_{2}$ is not. $H_{2}$ deforms continuously onto a figure 8 , not onto a point.

In the second picture it looks like you are cutting the torus into two cylinders. A cylinder is not contractible. It deforms continuously onto a circle.

These deformations show that the second real homology group of each of the pieces $H_{1,2}$, and the two cylinders $A$ and $B$ is zero. From De Rham's Theorem (for smooth manifolds with boundary), the Chern form is exact on each of them. In your notation, for each region $R$ there is a 1 form $A_{R}$ such that $dA_{R} = F$ on $R$.

This proof does not require showing that the bundle is trivial over each region.

- For any smooth n-plane bundle over a compact n-dimensional manifold, there is a smooth section that is zero except for a finite number of isolated zeros. These zeros can be chosen to lie in any open subset of the manifold. So if one chooses all of the zeros to lie in for instance $H_{1}$ then the section is non-zero on $H_{2}$. If the zeros are chosen to lie in $A$ then the section is non-zero over $B$. In the case of a complex line bundle over a surface e.g. the torus, there is a second linearly independent section with the same zeros.

- The argument that the bundle is trivial over $H_{1}$ because $H_{1}$ is contractible has a generalization that applies to other regions that are not contractible. The theorem is that if $f:X→Y$ is a homotopy equivalence between paracompact topological spaces, then every bundle over $X$ is an induced bundle $f^{*}(V)$of a bundle over $Y$. The projection map, $p$ of the cylinder $A$ or $B$ onto one of its boundary circles is a homotopy equivalence. Every bundle over the cylinder is an induced bundle $p^{*}(V)$of a bundle $V$ over the circle. Since the only oriented $U(1)$ bundle over the circle is trivial, it follows easily that an oriented $U(1)$ bundle over the cylinder is also trivial. For $H_{1}$ the projection onto any of its points is a homotopy equivalence so every bundle is induced from a bundle over a point. The projection of $H_{2}$ onto a figure 8 is a homotopy equivalence as well. Not sure about the vector bundles on a figure 8 . A reference for the theorem on homotopy equivalence is Hatcher, Vector Bundles and K-Theory. See Corollary 1.8 on page 21.

Thanks very much, you said "it follows easily that an oriented $U(1)$ bundle over the cylinder is also trivial", I have two questions
1, what about other bundles such as $U(N)$? The original text says for the second graph a vector bundle on patch A must be trivial, what is the reason for this ?
2, How do I know that I am dealing with a oriented bundle on the cylinder?

 

[lavinia]

Thanks very much, you said "it follows easily that an oriented $U(1)$ bundle over the cylinder is also trivial", I have two questions
1, what about other bundles such as $U(N)$? The original text says for the second graph a vector bundle on patch A must be trivial, what is the reason for this ?
2, How do I know that I am dealing with a oriented bundle on the cylinder?

There are only two circle bundles over the circle - the torus and the Klein bottle. The torus is trivial, the Klein bottle is not.

The induced bundle of a trivial bundle is trivial so the induced bundle of the trivial bundle over the circle under the projection map is the trivial bundle over the cylinder.

The pull back of the Klein bottle under the projection map is unorientable (the transition functions are still reflections around an axis) and so can not be a $U(1)$ bundle.

 

[lavinia]

Thanks very much, you said "it follows easily that an oriented $U(1)$ bundle over the cylinder is also trivial", I have two questions
1, what about other bundles such as $U(N)$? The original text says for the second graph a vector bundle on patch A must be trivial, what is the reason for this ?
2, How do I know that I am dealing with a oriented bundle on the cylinder?

I think this argument is right. Please correct it if it is wrong.

Whenever a principal bundle has a section, it is trivial. If $s:X→P$ is a section of a principal bundle over $X$ with group $G$ then the map $H:X×G→P$ defined by $H(x,g) = s(x)⋅p$ is a homeomorphism of the Cartesian product $X×G$ onto $P$.

A $U(n)$ bundle over a circle always has a section. Put a connection on the bundle and let $u(x):[0,2π]→P$ parallel translate an arbitrary point $p_0$ in $P$ around the circle. It may happen that this is not a closed curve in $P$ since it may return to a different point $p_1$ in the fiber above the starting point $x_0$. Since $U(n)$ acts transitively on the fiber above $x_0$ there is an element $α$ that carries $p_1$ to $p_0$ i.e. $p_1⋅α=p_0$. Choose a path $c(x)$ in $U(n)$ that connects the identity element to $α$ over the interval $[2π-ε,2π]$ for some small $ε$ and which is the identity over the interval $[0,2π-ε]$. This can be done because $U(n)$ is path connected. Then $u(x)⋅c(x)$ is a section of $P$ since $u(0)⋅c(0) = p_0⋅$identity $= p_0$ and $u(2π)⋅c(2π) = p_1⋅α=p_0$.

- I gave an argument why a complex line bundle is trivial over $A$ and $B$.