- #1
Clueless
- 26
- 2
This has been confusing me for an entire hour or so.
The momenergy vector is defined as mass*((spacetime displacement)/(proper time)). I understand this as much, but I don't know how to apply it to situations. The following snapshot is from a question about a photon colliding with a stationary electron and being backscattered.
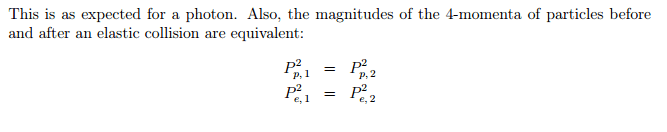
I don't understand how the conclusion about the magnitudes of the momenergy being the same can be drawn from knowing that an elastic collision has occured. Kinetic energy is when total kinetic energy is conserved in the collision. But how does that translate to the invariance of momenergy vectors? There is something I am missing, but I don't know what.
The momenergy vector is defined as mass*((spacetime displacement)/(proper time)). I understand this as much, but I don't know how to apply it to situations. The following snapshot is from a question about a photon colliding with a stationary electron and being backscattered.
I don't understand how the conclusion about the magnitudes of the momenergy being the same can be drawn from knowing that an elastic collision has occured. Kinetic energy is when total kinetic energy is conserved in the collision. But how does that translate to the invariance of momenergy vectors? There is something I am missing, but I don't know what.