Where are the pressure nodes on a standing acoustic wave in water?

[bubble-flow]

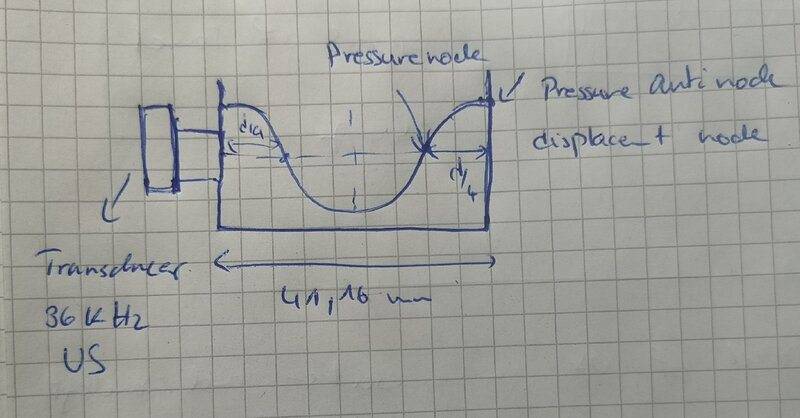
I have calculated the wave length of a 36 kHz acoustic wave in 20 °C water to be around 41.16mm.
Suppose I have a transducer that produces a 36 kHz acoustic wave and a small water container with a length of 41.6 mm. How will the standing acoustic wave look like, which is produced by the reflection of the incident ultrasound wave upon hitting the hard boundary (plexiglas wall) of the container?

I am not sure but as far as I have understood, the resulting standing wave has to have a pressure anti-node (displacement node) at the rigid boundary, which is the container wall, as the wall will not be able to oscillate. Does this mean that I draw one wave length backwards from the container wall and get to the transducer, which will result in another pressure anti-node on the transducer side?
Is the incident wave being emitted from the transducer completely ignored and only the standing acoustic wave plays a role in the container?
Also, am I understanding this correctly? On a pressure anti- node, the pressure changes with time , oscillating +- around the hydrostatic pressure and on a pressure node, the pressure remains contant (only hydrostatic pressure)?

I have included a simple sketch of this constellation.

Thank you for your help.

 

[hutchphd]

I believe that is a useful and correct description (the definition of dynamic and static pressure is always fraught). You understand I think that the Rayleigh waves at the surface are somewhat exotic creatures. But the pressure must support the water above.

 

[Mister T]

You will not have a displacement node at the precise position of the transducer. It'll be close, though.

 

[tech99]

The transducer will initially supply energy to allow the standing wave to build up over many cycles, until the standing wave has sufficient amplitude that the losses in the resonator absorb all the transducer power.

 

[sophiecentaur]

You will not have a displacement node at the precise position of the transducer. It'll be close, though.

This is true for any resonator. In order for Energy to enter the system there needs to be a real (resistive) component in the input and that implies a phase shift at reflection by the input port that's not Zero or 180 degrees - so there can't be a precise Node or Antinode exactly there.

 

[tech99]

My understanding is that the displacement and pressure standing waves are for the most part in time quadrature, having 90 degrees phase difference. However, as we move across a node, the phase rapidly changes by 180 degrees in a very short distance. Within this region the two are in phase, and we are seeing the resistive component of the resonator. So a transducer in this position will see a resistive load, and will also apply a resistive load to the resonator.

 

[sophiecentaur]

the displacement and pressure standing waves are for the most part in time quadrature, having 90 degrees phase difference.

The higher the Q, the nearer they are to quadrature. It's all just like the electrical equivalent but the effective location of the transducer is hard to specify because of its impedance.

Rayleigh waves at the surface are somewhat exotic

Too 'ard guv, afaiac. I understood that Rayleigh Waves are more a phenomenon in solids but there is bound to be more displacement of water near the surface and then you could get coupling into 'gravity waves' which are many orders of magnitude slower. My only experience of ultrasonic waves in water is in a cleaning bath and I seem to remember standing waves appearing on the surface - but they could be due to some other effect.

 

[hutchphd]

My understanding is that the displacement and pressure standing waves are for the most part in time quadrature,

That is true. For the waves near the interface (using Airy's solution) the pressure manifests as an additional transverse (upward) displacement of the surface which is in phase with the "pressure wave". Motion of the surface molecule of water is therefore circular (elliptical) as the wave (or waves) pass. For the standing waves I believe the net displacement at the surface to be mostly vertical .
Its very pretty math.