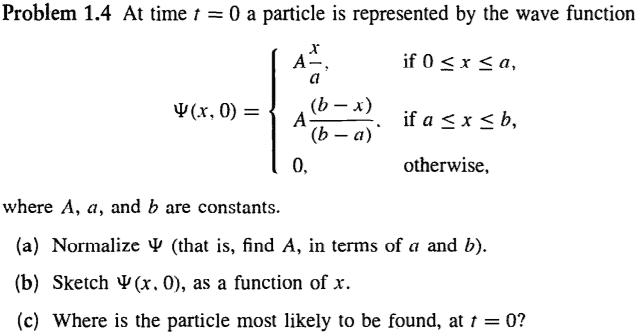Where is a particle most likely to be? (Griffiths Quantum Mechanics)

[blackbeans]

Homework Statement

Hi there, it seems more convenient to post a picture of the problem in question. More specifically, problem 1(c).

Relevant Equations

the schrodinger equation.

The wave function described seems impossible. Wave functions have to be differentiable at all points, right? Otherwise they don't represent a physically realizable state. The wave function in the example isn't differentiable at x=A, the maximum point. Also, for problem (c), I know it's visually simple to see the answer, but for a more general case, how would i find the coordinate where the "particle is most likely to be"? Would I take the derivative of |psi|^2 or |psi| to find the absolute maxima? Do they provide the same result? Is there a simpler method?

 

[PeroK]

Theoretically, wave functions need only be square integrable. You could, however, look at this sort of function an idealised approximation to a function that would have a differentiable maximum.

As you state, the modulus squared of the wave function represents the PDF of the particle's position. You calculate the maximum as you would for any function, using calculus or otherwise.

 

[blackbeans]

I see. I just assumed that the wave function had to be differentiable everywhere, since its derivative shows up in the Schrödinger Eq. Thank you!

 

[PeroK]

I see. I just assumed that the wave function had to be differentiable everywhere, since its derivative shows up in the Schrödinger Eq. Thank you!

Technically it's better if it is differentiable. But differentiable almost everywhere is probably good enough