Where Should Particle C Be Placed to Balance Gravitational Forces on Particle A?

[TS656577]

Homework Statement

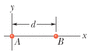
One dimension. In Fig. 13-33, two point particles are fixed on an x-axis separated by distance d. Particle A has mass mA and particle B has mass 7.00 mA. A third particle C, of mass 75.0 mA, is to be placed on the x-axis and near particles A and B. In terms of distance d, at what x coordinate should C be placed so that the net gravitational force on particle A from particles B and C is zero?

Homework Equations

F=sqrt((GMm)/r^2) Where G=6.67E-11

The Attempt at a Solution

I know that M=75 and m=7. Multiplying that by 6.67E-11 I got 3.5E-8/r^2. If i set that equal to 0, then I the r to disappear

 

[G01]

Here you are going to have two forces on A, the force from B and the force from C.

HINT:

You want the net force on A to be zero:

\Sigma F = 0

Can you write the net force in terms of the force from B and C?

 

[TS656577]

So would it be the gravitational potential energy between A and C plus the GPE of A and B and add them? and set that = to F(theta)? because in the picture, there is no C

 

[G01]

Personally, I think it would be more straight forward to work with Forces here and not potential energies. Also, I do not know why you are using a theta variable, which I assume is an angle. All three masses will be on the same line. There is no C in the picture because you need to figure out where to place it so the net force on A is 0 N. That is the problem.

Try answering these questions to start:

Can you give me a formula for the force from B, in terms of the distance d?

If so, then can you give me a formula for the force from C in terms of x, the position you want to find?

If you can do that as well can you write the net force in terms of the above quantities you just found?

 

[Feldoh]

The forces need to cancel out. This means that the force of c on a and b on a must be equal and opposite, right? No need to work with angles as G01 said, since you're restricted to one dimension.