rbmartel
- 4
- 2
- TL;DR
- In order to find the resultant force applied to a submerged vertical wall, which area should I consider?
Let's say we have a tank filled with water only half way up. I want to calculate the force being applied by the liquid on one of the walls, that's F = P.A. For the area (A), should I consider the area of the entire wall (H.L), or only the area of the wall that's in contact with the liquid ((H/2).L).
I'm having a hard time trying to understand if I should or shouldn't include in the calculations the part of the wall that is not in contact with the water.
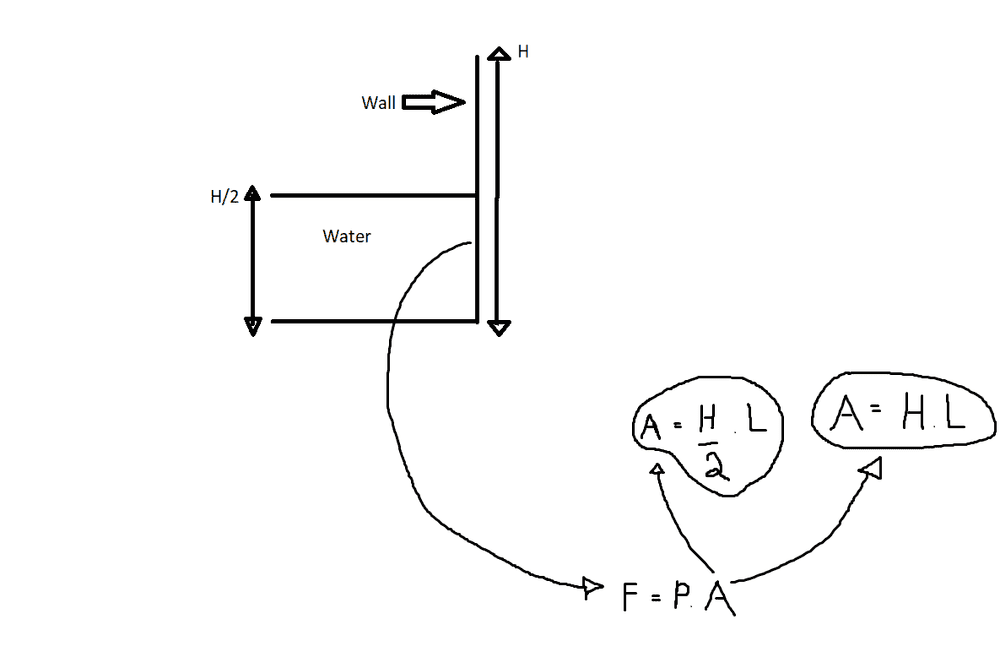
I'm having a hard time trying to understand if I should or shouldn't include in the calculations the part of the wall that is not in contact with the water.