evinda
Gold Member
MHB
- 3,741
- 0
Also,to see if I understood it,I tried an other example.
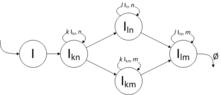
The grammar that is given is this:
w\epsilon \left \{ k,l,m,n \right \}^{*}:I\rightarrow I_{kn},I_{kn}\rightarrow kI_{kn}n|I_{ln}|I_{km},I_{ln}\rightarrow lI_{ln}n|I_{lm},I_{km}\rightarrow kI_{km}m|I_{lm},I_{lm}\rightarrow lI_{lm}m|\O ,
and I found that it generates the following strings:
I\rightarrow I_{kn}\rightarrow k I_{kn} n \rightarrow kknn
I\rightarrow I_{ln}\rightarrow l I_{kn} n \rightarrow llnn
I\rightarrow I_{km}\rightarrow k I_{km} m \rightarrow kkmm
I\rightarrow I_{lm}\rightarrow l I_{kn} m \rightarrow llmm
Is this right??
The grammar that is given is this:
w\epsilon \left \{ k,l,m,n \right \}^{*}:I\rightarrow I_{kn},I_{kn}\rightarrow kI_{kn}n|I_{ln}|I_{km},I_{ln}\rightarrow lI_{ln}n|I_{lm},I_{km}\rightarrow kI_{km}m|I_{lm},I_{lm}\rightarrow lI_{lm}m|\O ,
and I found that it generates the following strings:
I\rightarrow I_{kn}\rightarrow k I_{kn} n \rightarrow kknn
I\rightarrow I_{ln}\rightarrow l I_{kn} n \rightarrow llnn
I\rightarrow I_{km}\rightarrow k I_{km} m \rightarrow kkmm
I\rightarrow I_{lm}\rightarrow l I_{kn} m \rightarrow llmm
Is this right??