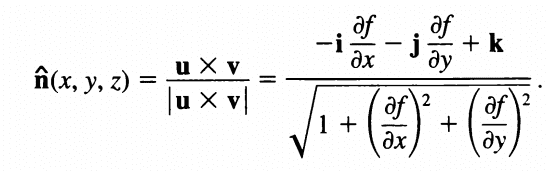SUMMARY
The correct unit normal vector of a surface is context-dependent, specifically defined by the orientation of the surface in relation to a closed region. Both vectors presented in the discussion are valid unit normals; however, their designation as "inward" or "outward" relies on the overall orientation of the surface. The sign of the normal vector is crucial, as it determines the directionality of the vector. A continuous normal vector field exists only for orientable surfaces, exemplified by the Mobius Strip, which demonstrates a discontinuous normal vector field.
PREREQUISITES
- Understanding of unit normal vectors in differential geometry
- Familiarity with the concepts of surface orientation and integrability
- Knowledge of gradient and cross product calculations
- Basic principles of orientability in topology
NEXT STEPS
- Study the implications of surface orientation in vector calculus
- Learn about the properties of orientable vs. non-orientable surfaces
- Explore the application of normal vectors in surface integrals
- Investigate the mathematical definition and examples of the Mobius Strip
USEFUL FOR
Mathematicians, physicists, and computer graphics professionals who require a deep understanding of surface geometry and normal vector applications in their work.