Doubt on the derivation of an equation for a surface integral

[Hamiltonian]

TL;DR Summary

doubt in the derivation of the expression for calculating the surface integral for a function F.

this method of derivation is approximating the function using a polyhedron.

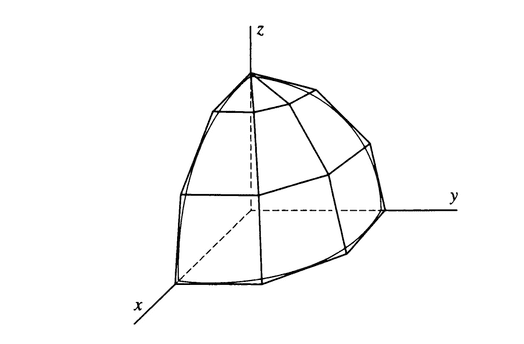
concentrating on one of the surfaces(say the L'th surface which has an area $\Delta S_l$ and let $(x_l,y_l,z_l)$ be the coordinate of the point at which the face is tangent to the surface and let $\hat n$ be the unit normal vector)

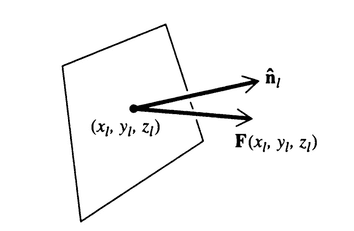
the area of this surface is given by $F(x_l, y_l, z_l).\hat n_l \Delta S_l$
on adding all of these we get,

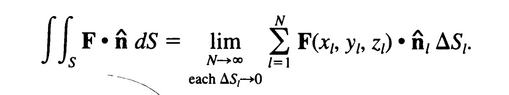
my doubt in this derivation is why is there a dot product being taken between the vectors and then multiplied by the area(basically I don't understand why this equation, $F(x_l, y_l, z_l).\hat n_l \Delta S_l$ give the area as shouldn't the summation of all the $\Delta S_l$ simply be equal to the surface area of the function??)

 

[etotheipi]

the area of this surface is given by $F(x_l, y_l, z_l).\hat n_l \Delta S_l$
on adding all of these we get,

No - the area of that little piece is just $\Delta S_l$, whilst the (so-called) vector area of that little piece is $\hat{n} \Delta S_l$. The term $\vec{F} \cdot \hat{n} \Delta S_l$ is the "flux" of the vector field through that little piece, and by extension$$\Phi = \int_{\Sigma} \vec{F} \cdot \hat{n} dS$$is the flux out of the surface $\Sigma$. For example, consider some fluid with velocity field $\vec{v}(\vec{r})$. The volume of fluid that passes through the little piece of area $dS$ per time $dt$ is $\vec{v} \cdot \hat{n} dS = (v\cos{\theta}) dS$. Note that this is the volume of an oblique prism of base area $dS$, slant length $v$ and height $v\cos{\theta}$ between the faces at either end, which contains the fluid that has flown through the element per $dt$.

The area of a surface is also $\int_S dS$, whilst the vector area of a surface is $\int_S \hat{n} dS$. N.B. that the vector area of a closed surface is zero.

[P.S. In many general cases, for a current density $\vec{J} = \rho \vec{v}$ associated with an extensive quantity $Q$ where $\rho = \frac{\partial Q}{\partial V}$, if ´$Q$ isn't being 'generated' or 'destroyed' inside the surface, you can say$$\frac{dQ_{\Omega}}{dt} = -\int_{\partial \Omega} \rho \vec{v} \cdot \hat{n} dS$$

 

[Hamiltonian]

No - the area of that little piece is just $\Delta S_l$, whilst the (so-called) vector area of that little piece is $\hat{n} \Delta S_l$. The term $\vec{F} \cdot \hat{n} \Delta S_l$ is the "flux" of the vector field through that little piece, and by extension$$\Phi = \int_{\Sigma} \vec{F} \cdot \hat{n} dS$$is the flux out of the surface $\Sigma$.

I still don't understand how

this is derived.
(I understand the mistake in my previous post. how exactly do you get the surface area from the flux?)

 

[etotheipi]

Nothing's really been derived here, I think that's sort of the definition of the flux of a vector field through a surface. But I tried to give some motivation by looking at volumetric flow rates, maybe have a look at this figure:

You'll notice that the volume inside that oblique cylinder is $\vec{u} \delta t \cdot \hat{n} \delta S$, from which you might deduce the volumetric flow rate through a surface is $\dot{V} = \int_{\Sigma} \vec{u} \cdot \hat{n} dS$.

Surface area is a simpler concept than flux, since the surface area of a surface is just $\int_{\Sigma} dS$. If you want the vector surface area instead, then you can just consider $\int_{\Sigma} \hat{n} dS$.

 

[Stephen Tashi]

(I understand the mistake in my previous post. how exactly do you get the surface area from the flux?)

The main purpose of a surface integral is not to find a surface area. A surface integral computes the flux of a vector field through a surface.

Imagine we have pipe with a uniform cross section and water is flowing through it at a constant velocity. The flux of the water is measured in units like (liters per second)/ (square cm) and we would (theoretically) measure the flux by measuring the rate at which water flows through a surface that is a cross section of the pipe - i.e. a surface perpendicular to the sides of the pipe. Suppose we cannot measure the flow through a surface perpendicular to the sides of the pipe, but instead must measure it through a planar surface that is not perpedicular to the sides of the pipe. The dot product in a surface integral is used to correct for the fact we are not measuring the flow through a surface perpendicular to the sides of the pipe - or, as another way of looking at it, that we are not measuring flow in a direction perpendicular to the surface.