Homework Help Overview
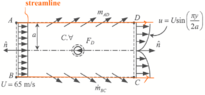
The discussion revolves around the behavior of fluid flow in relation to the continuity equation and streamlines, particularly in the context of steady flow and turbulent flow. Participants are exploring why mass can cross streamlines despite the assumption that streamlines represent paths of fluid particles in steady flow.
Discussion Character
- Conceptual clarification, Assumption checking, Mixed
Approaches and Questions Raised
- Participants are questioning the nature of fluid flow around obstacles, particularly whether fluid elements can cross streamlines in steady flow. Some suggest that mass can cross streamlines in turbulent flow, while others argue that in steady flow, streamlines should not allow for such crossing. There are discussions about the implications of mass conservation and the behavior of fluid particles as they encounter obstructions.
Discussion Status
The discussion is ongoing, with participants providing various perspectives on the behavior of fluid elements in relation to streamlines. Some have offered detailed explanations and analogies to illustrate their points, while others are seeking clarification on the concepts being debated. There is no explicit consensus, but several productive lines of reasoning are being explored.
Contextual Notes
Participants are grappling with the definitions of steady and turbulent flow, as well as the implications of the continuity equation in the context of fluid dynamics. The presence of diagrams in the discussion suggests that visual aids may be influencing the understanding of the concepts being discussed.