NODARman
- 57
- 13
- TL;DR
- .
Can anyone explain to me why the second one is the right?
(See the attachment)
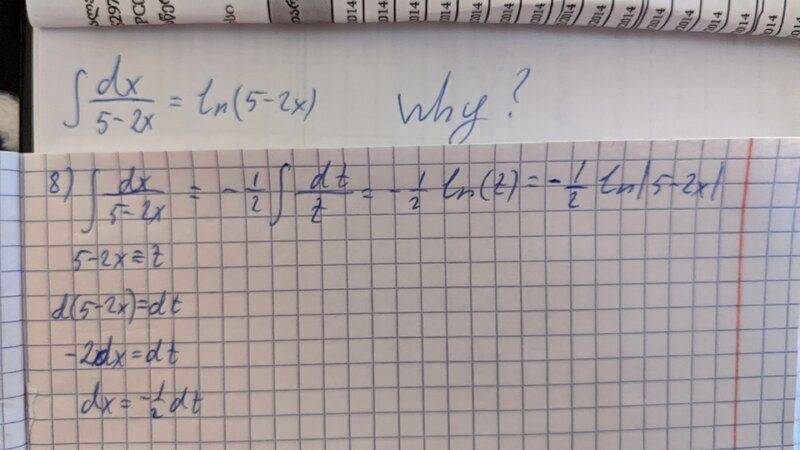
(See the attachment)
Why can't we just integrate a simple function?
Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
3 replies · 2K views
- 29,796
- 21,619
The integral is the anti-derivative. What happens when you differentiate ##\ln(5 - 2x)##?
- 5,706
- 1,592
Your question is where does the ##-1/2## multiplier come from?
NODARman
- 57
- 13
Just got itPeroK said:
