parshyaa
- 307
- 19
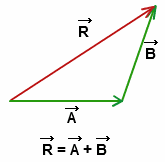
Do we have any proof to show that we can represent the addition of two vectors like this, i mean do we have proof for triangle law of vector addition(or its a law that is why we can't have its proof, then please give me a satisfying reason for this)