Why Did I Get a Different Average Velocity Calculation for the Particle?

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

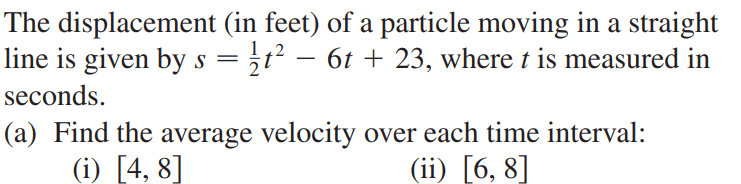
The solution to (a)(i) is 0 ft/s. However I got -4 ft/s.

The formula I used was,
$v_{avg} = \frac{s_f - s_i}{t_f - t_i}$
$v_{avg} = \frac{\frac{1}{2}t^2_f - 6t_f + 23 - \frac{1}{2}t^2_i - 6t_i + 23}{t_f - t_i}$
$v_{avg} = \frac{ \frac{1}{2}(t^2_f - t^2_i) - 6(t_f - t_i)}{t_f - t_i}$

If someone could please point out what I did wrong, that would be much appreciated.

Many thanks!

 

[Halc]

Can't you just plug in the times in question to get the two positions in question? All the algebra seems unnecessary.

That aside, I don't see where the -4 comes from. Your bottom line seems correct.

 

[member 731016]

Can't you just plug in the times in question to get the two positions in question? All the algebra seems unnecessary.

That aside, I don't see where the -4 comes from. Your bottom line seems correct.

Thank you for your reply @Halc!

Sorry, my mistake. The formula that I forgot to write above was $v_{avg} = \frac{1}{2}\Delta t - 6$ because I mistakenly cancelled some of the change in times.

Many thanks!

 

[FactChecker]

1) You should include some parenthesis in your second line where you have substituted for $s_i$.

The formula that I forgot to write above was $v_{avg} = \frac{1}{2}\Delta t - 6$

2) This looks wrong to me. I think it should be $v_{avg} = \frac{\frac{1}{2}(t_f+t_i)(t_f-t_i) - 6(t_f-t_i)}{(t_f-t_i)}= \frac{1}{2}(t_f+t_i) - 6$.
3) You could always follow the advice @Halc gave in post #2 of just calculating the initial and final positions. At least use that to check your algebra.

 

[BvU]

$v_{avg} = \frac{ \frac{1}{2}(t^2_f - t^2_i) - 6(t_f - t_i)}{t_f - t_i}$

If someone could please point out what I did wrong, that would be much appreciated.

Formula seems correct. Did you simply forget the $1\over 2$ ?

[edit] never mind

 

[haruspex]

$v_{avg} = \frac{\frac{1}{2}t^2_f - 6t_f + 23 - \frac{1}{2}t^2_i - 6t_i + 23}{t_f - t_i}$

Typo: Missing parentheses around the $t_i$ terms, leading to wrong signs.

The formula that I forgot to write above was $v_{avg} = \frac{1}{2}\Delta t - 6$

What is $\frac{x^2-y^2}{x-y}$?

 

[member 731016]

1) You should include some parenthesis in your second line where you have substituted for $s_i$.

2) This looks wrong to me. I think it should be $v_{avg} = \frac{\frac{1}{2}(t_f+t_i)(t_f-t_i) - 6(t_f-t_i)}{(t_f-t_i)}= \frac{1}{2}(t_f+t_i) - 6$.
3) You could always follow the advice @Halc gave in post #2 of just calculating the initial and final positions. At least use that to check your algebra.

Thank you for your reply @FactChecker ! I agree.

 

[member 731016]

Formula seems correct. Did you simply forget the $1\over 2$ ?

[edit] never mind

Typo: Missing parentheses around the $t_i$ terms, leading to wrong signs.

What is $\frac{x^2-y^2}{x-y}$?

Thank you for your replies @BvU and @haruspex!

Yes, sorry I forgot the parentheses. $\frac{(x + y)(x - y)}{x - y} = x + y$

Many thanks!