StandardsGuy
- 148
- 9
We are told that planets and comets orbit the sun in an ellipse (Kepler's 3 laws) as shown below:
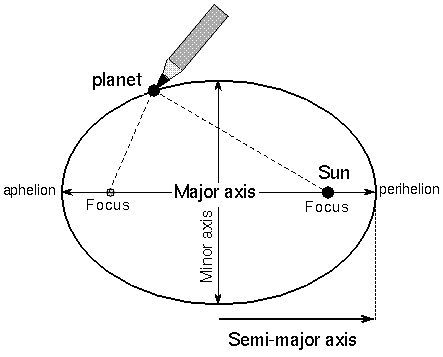
We are also told that according to Einstein's theory of gravity, there is no force applied. Implied is that the planets move in straight lines through curved space. We know that the effect of gravity drops off as the square of the distance. Why then does the planet follow the exact same curvature on the far away focus (where the space-time curvature is relatively flat) that it does by the sun (where the curvature is extreme)?
We are also told that according to Einstein's theory of gravity, there is no force applied. Implied is that the planets move in straight lines through curved space. We know that the effect of gravity drops off as the square of the distance. Why then does the planet follow the exact same curvature on the far away focus (where the space-time curvature is relatively flat) that it does by the sun (where the curvature is extreme)?