- #1
kayan
- 37
- 0
This question is regarding the dependence of Planck's law for black-body (BB) radiation intensity (or integrating over a hemisphere, the emissive power, E = pi * I).
Physically speaking, why is it that a BB emitting in a medium with n>1 (n being index of refraction) emits a higher power/area than the same BB (same T, same everything) in a vacuum (n=1)?
Obviously, I can just plug greater values of n into Planck's law to see this mathematically, and I have done that in the plot attached below for n values 1 (red, bottom), 1.25 (blue, mid), 1.50 (green, top). However, how can I make sense of this trend? It seems counter intuitive that if radiation has to travel through a medium with a higher n (slower speed), then the power increases? I've tried over and over to rationalize this trend using both photon and wave behavior, but cannot come to a rationale that makes sense. For example, in the photon perspective, higher n means each photon travels slower in the medium, which means that the spatial photon intensity increases, however, since the photons are traveling slower, this also means that whatever object they are irradiating, they would take longer to reach that object (even though they are closer together spacially), hence, there wouldn't be a change.
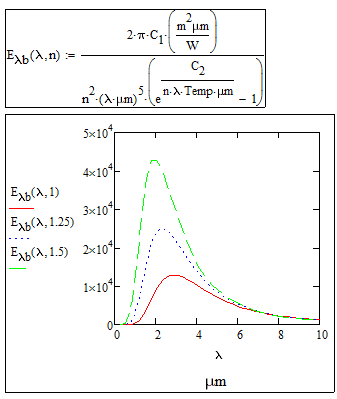
Physically speaking, why is it that a BB emitting in a medium with n>1 (n being index of refraction) emits a higher power/area than the same BB (same T, same everything) in a vacuum (n=1)?
Obviously, I can just plug greater values of n into Planck's law to see this mathematically, and I have done that in the plot attached below for n values 1 (red, bottom), 1.25 (blue, mid), 1.50 (green, top). However, how can I make sense of this trend? It seems counter intuitive that if radiation has to travel through a medium with a higher n (slower speed), then the power increases? I've tried over and over to rationalize this trend using both photon and wave behavior, but cannot come to a rationale that makes sense. For example, in the photon perspective, higher n means each photon travels slower in the medium, which means that the spatial photon intensity increases, however, since the photons are traveling slower, this also means that whatever object they are irradiating, they would take longer to reach that object (even though they are closer together spacially), hence, there wouldn't be a change.