Guidestone
- 93
- 5
Homework posted in wrong forum, so no template
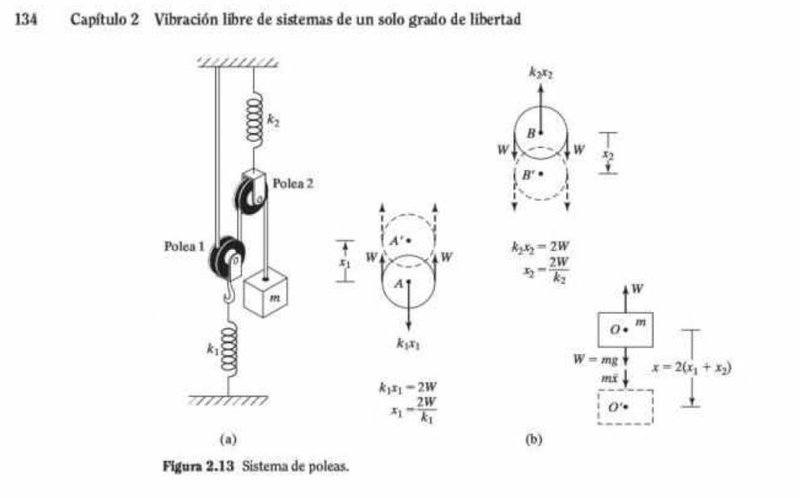
Hey guys, I'm wondering why the displacement of the mass mounted in this setup is 2(x1+x2)?. I'm assuming that when the pulley rotates(when the mass is pulled downwards) the distance between the initial point and the end point of its center and the distance traveled by the mass are equal, meaning that both the mass and the pulley moved the same distance. However, I don't know what other phenomenon is adding displacement to the mass To make it double. I would be really grateful if you clarify on this matter.