SUMMARY
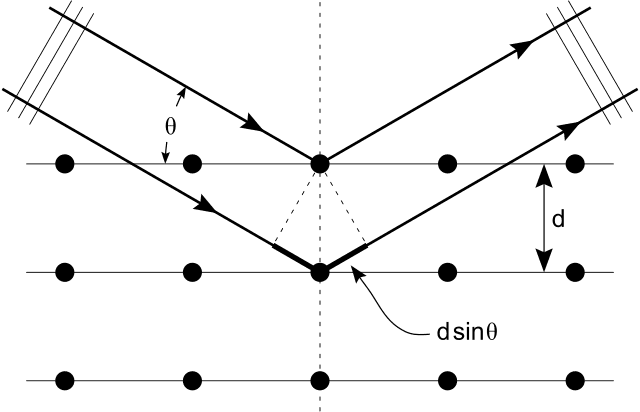
The scattering of X-rays at angle 2dsinθ is fundamentally linked to interference theory, specifically through the Bragg Reflection Formula. When a coherent beam illuminates a regular array of scatterers, constructive interference occurs only at specific angles where the scatterers are in phase. This results in defined maxima in scattered intensity, which are crucial for accurate diffraction analysis. The depth and width of the crystal enhance the sharpness of these maxima, while incorrect angles of incidence disrupt coherent addition of scattered waves.
PREREQUISITES
- Understanding of interference theory and wave behavior
- Familiarity with Bragg Reflection Formula
- Knowledge of X-ray diffraction principles
- Basic concepts of phase relationships in wave mechanics
NEXT STEPS
- Study Laue's theory of X-ray diffraction for alternative scattering models
- Explore Young's Slits experiment to understand foundational interference patterns
- Investigate the application of Bragg's Law in various scattering processes
- Learn about phase coherence in wave mechanics and its implications in diffraction
USEFUL FOR
Physics students, materials scientists, and professionals involved in X-ray crystallography or any field utilizing wave interference principles.