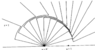
This picture tries to give an intuitive reason that an accelerated charge radiates. Imagine that you have a charged particle moving along the x-axis at a constant speed. The electric field associated with that situation points toward the moving particle. Now, at some point, the particle abruptly halts. Nearby the particle, the electric field points toward the particle. But the information that the particle's motion has changed hasn't reached far-away places, so the electric field continues to point toward where the particle would have been, if it kept traveling at the same speed. Because electric fields have to be continuous in vacuum, there must be a transition region, spreading out spherically at the speed of light, where the electric field rapidly changes from one configuration to the other. This region of rapidly changing electric (and magnetic, since that changes, too) fields is a spherical burst of electromagnetic radiation. This is shown in the following picture:
View attachment 225442
To the extent that this intuitive picture is accurate, I think we can conclude that there is no radiation as viewed from a reference frame in which the situation is static. If the electric field far away from the charge isn't changing with time, then there shouldn't be a need for the radiation, which sort of acts like a "correction" to the field that propagates at the speed of light.
The interesting case is a charged particle undergoing constant proper acceleration. From the point of view of a Rindler observer, the situation is static, so there should be no radiation. But from the point of view of an inertial observer, the situation is not static, and it's also not the constant-velocity case. I'm not sure what the electric field looks like to the inertial observer.
A charge at rest on a planet shouldn't radiate, according to this heuristic, because the distant electric field is unchanging (in the frame in which the situation is static, which is someone at rest in the Schwarzschild coordinate system).