fitz_calc
- 41
- 0
This is an example I found online. I know how to get to this:
fitz_calc said:
This is an example I found online. I know how to get to this:, but why is 3-4x brought into the problem? sorry for the newbie questions tonight but my notes from class don't really cover the material very well, thanks.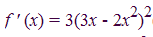
rocophysics said:that's a great way Casey, makes a lot of sense too; exactly how i learned logs
fitz_calc said:ok i think I'm getting it. i tried a homework problem:
y=(4+x^4)^5 => u=g(x)=4+x^4 , f(u)=u^5
then f(x)=f(g(x)) => 5u^4 * (4x^3) => 5(4+x^4)^4 * (4x^3)
* a bit of confusion here -- why can't I multiply the 5 by (4+x^4)^4?
I know the answer is 20x^3 (4+x^4)^4 but can't figure out why the 5 isn't distributed in the last step, thanks