fitz_calc
- 41
- 0
This is an example I found online. I know how to get to this:
The discussion centers on the application of the chain rule in calculus, specifically in the context of differentiating composite functions. The example provided, f(x)=(3x-2x^2)^3, illustrates how the derivative f'(x) incorporates the term 3-4x through the chain rule. Participants clarify that the chain rule involves taking the derivative of the outer function and multiplying it by the derivative of the inner function. This method is essential for correctly applying derivatives to functions composed of multiple layers.
PREREQUISITESStudents learning calculus, educators teaching differentiation techniques, and anyone seeking to improve their understanding of the chain rule and composite functions in mathematical analysis.
fitz_calc said:
This is an example I found online. I know how to get to this:, but why is 3-4x brought into the problem? sorry for the newbie questions tonight but my notes from class don't really cover the material very well, thanks.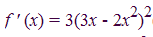
rocophysics said:that's a great way Casey, makes a lot of sense too; exactly how i learned logs
fitz_calc said:ok i think I'm getting it. i tried a homework problem:
y=(4+x^4)^5 => u=g(x)=4+x^4 , f(u)=u^5
then f(x)=f(g(x)) => 5u^4 * (4x^3) => 5(4+x^4)^4 * (4x^3)
* a bit of confusion here -- why can't I multiply the 5 by (4+x^4)^4?
I know the answer is 20x^3 (4+x^4)^4 but can't figure out why the 5 isn't distributed in the last step, thanks