druidwoody
- 1
- 0
This homework problem was originally posted in another forum so there is no template
Hi,
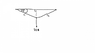
I have a revision book that has an example in it for the tension on a rope
if a 20 Newton force is hanging on the centre of a rope suspended between two points.
The rope dips 25 Degrees either side. So effectively an upside down pair of right angled triangles is formed.
The Hypoteneuse being 25 Degrees down.
http://d:\Rope-example.png
The Revision textbook Example shows how to find the Tension
2TCos65(Degrees)=20N
and shows T works out to be 24 Newtons.
I can not see where the 2TCos65=20 comes from, at least its not intuitive to me.
So I figured it out with a simultaneous equation. T1 = left T2 = right
Where the forces are worked out, asuming everything is static.
1) T1Cos25 + T2Cos65=0
2) T1Sin65 + T2Sin25=20N
From 1)
3) T1=T2x0.466
From 2)
T1x0.966 + T2x0.422 = 20
Substitute for T1 from 3)
T2x0.466x0.906 + T2x0.422 = 20
=> T2 x 0.844 = 20
Therfore T2 = 23.69N which is close enough to 24 Newtons in the example. I assume this is correct? (Maybe the book is wrong too?)
I was pleased with myself, until I checked by substituting T2 back fot T1 to check T1 was the same. I assume T1 and T2 are equal tensions.
But it is not, which I found very puzzling. I get about 11 Newtons. i.e put 23.69 in place of T2 in 3) above.
Can anyone explain what I have done wrong? Signs perhaps?, unfortunately my math is not the greatest.
Regards,
I have a revision book that has an example in it for the tension on a rope
if a 20 Newton force is hanging on the centre of a rope suspended between two points.
The rope dips 25 Degrees either side. So effectively an upside down pair of right angled triangles is formed.
The Hypoteneuse being 25 Degrees down.
http://d:\Rope-example.png
The Revision textbook Example shows how to find the Tension
2TCos65(Degrees)=20N
and shows T works out to be 24 Newtons.
I can not see where the 2TCos65=20 comes from, at least its not intuitive to me.
So I figured it out with a simultaneous equation. T1 = left T2 = right
Where the forces are worked out, asuming everything is static.
1) T1Cos25 + T2Cos65=0
2) T1Sin65 + T2Sin25=20N
From 1)
3) T1=T2x0.466
From 2)
T1x0.966 + T2x0.422 = 20
Substitute for T1 from 3)
T2x0.466x0.906 + T2x0.422 = 20
=> T2 x 0.844 = 20
Therfore T2 = 23.69N which is close enough to 24 Newtons in the example. I assume this is correct? (Maybe the book is wrong too?)
I was pleased with myself, until I checked by substituting T2 back fot T1 to check T1 was the same. I assume T1 and T2 are equal tensions.
But it is not, which I found very puzzling. I get about 11 Newtons. i.e put 23.69 in place of T2 in 3) above.
Can anyone explain what I have done wrong? Signs perhaps?, unfortunately my math is not the greatest.
Regards,