PainterGuy
- 938
- 73
Hi,
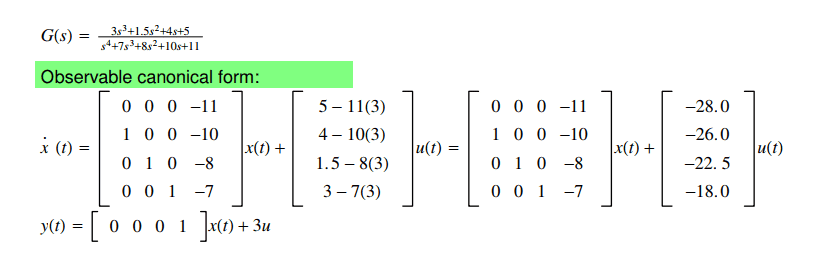
I found the above observable canonical form using this source:
https://www.mathworks.com/help/cont....html#mw_a76b9bac-e8fd-4d0e-8c86-e31e657471cc
I'm almost certain that I did do it correctly. But the code below gives me different values for B, C, and D. Could you please help me to understand what's going on? Which form is correct?
Output:

I found the above observable canonical form using this source:
https://www.mathworks.com/help/cont....html#mw_a76b9bac-e8fd-4d0e-8c86-e31e657471cc
I'm almost certain that I did do it correctly. But the code below gives me different values for B, C, and D. Could you please help me to understand what's going on? Which form is correct?
Matlab:
close all; clear all; clc;
num=[3 1.5 4 5];
den=[1 7 8 10 11];
G = tf([num], [den]) % conversion into transfer function in s
obs_canon = canon(G,'companion') % observable canonical form