ghwellsjr
Science Advisor
Gold Member
- 5,122
- 150
The above comment makes me ask you the same question I asked bobc2 (which he didn't answer):Fredrik said:The fact that you're denoting the S' coordinate of the right endpoint of the rod by x2' suggests that you didn't realize that you need to consider three events, not two.
There are only two events under consideration, not three or more. These are the end points of the moving stick in frame S and they must be simultaneous in that frame. The distance between the two events is L. In the rod's rest frame S', those two events are not simultaneous but since the rod is at rest, the difference in the x-coordinates of the two events is equal to the Proper Length of the rod, L0.ghwellsjr said:The whole point of the preceding posts in this thread is that in the frame in which the rod is moving, we pick a pair of events at the two ends of the stick that are simultaneous but in the rod's rest frame these events are not simultaneous. Is your sketch supposed to be illustrating the process described in the wikipedia article or are you showing some other method to illustrate length contraction?
I agree that there's too much information in bobc2's drawing but there's too much in yours too, as far as the number of events goes. The two events we care about are labeled A and B. C should not be shown as an event. Erase that dot and the C. If you try to show that there are two simultaneous events in frame S', then you have missed the whole point of the derivation. Events A and B are not simultaneous in frame S' and that's the way we want it to be.Fredrik said:I think there's just too much information in that diagram. (I didn't try to determine if that information is correct or not). I would prefer one with just the necessary information drawn in. Something like this:
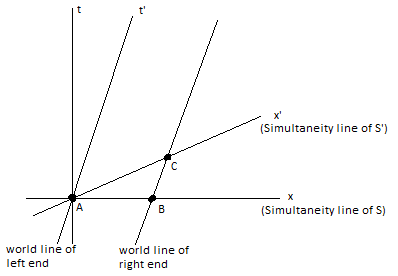
But that is (almost) the correct interpretation if you recognize that x'C is equal to x'B so you should have said ##L_0=x'_B-x'_A>x_B-x_A=L##. However, you really need to show the grid lines for the two frames, otherwise, it's impossible to tell what the value of x'B is or that it is larger than xB. The whole purpose of a Minkowski diagram is to show the two sets of coordinates for the two frames so that you can see that they are different for the two frames and it's those numbers that show that L is less than L0, not the fact that two line segments are actually drawn to two different lengths.Fredrik said:If you disregard my poor drawing skills (the slope of the x' axis isn't exactly right), the only problem with this diagram is that a person who doesn't understand that the scales on the axes are fixed by the invariant hyperbolas might interpret it as saying that ##L_0=x'_C-x'_A>x_B-x_A=L##.
You already stated the correct relationship between L and L0 at the end of post #17, why'd you change your mind? This last paragraph is all wrong. We don't need hyperbolic calibration curves, we just need marked grid lines. Why don't you or bobc2 draw a correctly annotated Minkowski diagram that illustrates the derivation of the length contraction that is the subject of this thread?Fredrik said:I would recommend section 1.7 in Schutz to anyone who's struggling with that. In particular fig. 1.11 at the bottom of page 17.
To see that the inequality actually goes the other way, what you have to do is to draw a curve of the form ##-t^2+x^2=\text{constant}## with the constant chosen so that the curve goes through C. The point where this curve intersects the x-axis will have coordinates (0,L0). This point will be to the left of B on the x axis. So ##L_0<L##.
