Why is Point A in Compression in a Simplified Crankshaft with a Load P?

Click For Summary

Discussion Overview

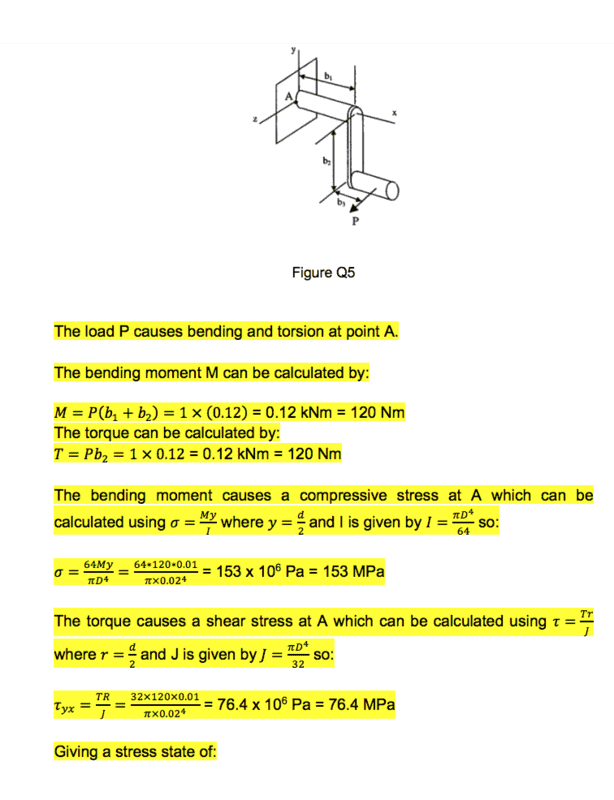
The discussion revolves around understanding why point A in a simplified crankshaft is considered to be in compression when subjected to a load P. Participants explore the mechanics of bending moments and stress distribution in beams, particularly focusing on the implications of point A's position relative to the beam's curvature.

Discussion Character

  • Technical explanation
  • Conceptual clarification
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • One participant expresses confusion about the classification of stress at point A, noting that both their calculations and the solutions indicate positive stress values, which they associate with tension.
  • Another participant explains that in bending, the concave portion of a beam is in compression while the convex portion is in tension, suggesting that point A is in the concave portion.
  • A different participant proposes visualizing the forces acting on point A by eliminating a section of the crankshaft to clarify the bending effects.
  • One participant questions how to determine if point A is in compression when it is located on the side of the beam, indicating a lack of clarity regarding the influence of load P on stress classification.
  • Another participant confirms that in a modified scenario where the load P acts downwards, point A would be in tension, emphasizing the importance of concave versus convex positioning rather than absolute top or bottom placement.
  • One participant acknowledges a previous misunderstanding and seeks clarification on the stress state of point A in different configurations of the beam.
  • A later reply points out that point A in the first diagram is not positioned the same as in the second diagram, suggesting that the context of the diagrams is crucial for understanding the stress state.

Areas of Agreement / Disagreement

Participants exhibit a mix of understanding and confusion regarding the stress state at point A, with some agreeing on the principles of bending while others remain uncertain about the implications of different load orientations and beam configurations. The discussion does not reach a consensus on the classification of stress at point A in all scenarios presented.

Contextual Notes

Participants express uncertainty about the definitions of tension and compression in relation to the position of point A and the effects of load P. There are unresolved questions regarding the application of bending theory to different configurations of the crankshaft.

yonese
Messages
15
Reaction score
1
Summary:: I'm stuck on a year 2 mechanics question. I have this simplified crankshaft with a load P at the end. The solutions to the exercise have said that point A is in compression due to a bending moment but I don't understand why that is. The solutions and my calculations have both come out with positive values for the stress at A, and I thought a positive value for stress = tension, negative = compression.

Screen Shot 2020-12-20 at 16.19.32.png
 

Attachments

  • Screen Shot 2020-12-19 at 14.59.13.png
    Screen Shot 2020-12-19 at 14.59.13.png
    15.3 KB · Views: 205
  • Screen Shot 2020-12-20 at 16.19.32.png
    Screen Shot 2020-12-20 at 16.19.32.png
    34.5 KB · Views: 207
Physics news on Phys.org
The moments (and forces) have directions that can be determined by the sign.

But for a beam in bending, you have the following situation:

image002.gif

beam_bending.png

When under the bending moment ##M##, the point on the convex portion (bottom) of the beam is in tension, but the concave portion (top) of the beam is in compression. The point A of your crankshaft would be in the concave portion.
 
  • Like
  • Informative
Likes   Reactions: yonese, berkeman and Lnewqban
Welcome, yonese! :cool:

If we eliminate section b2 of the crankshaft, could you see the direction of the forces acting on point A due to bending more clearly?

Signs are only an arbitrary convention.
 
  • Like
Likes   Reactions: yonese
Thank you! I hadn't thought of eliminating section b2, which does make it simplier to understand the forces acting on the beam. I can understand whether point A would be in compresssion or tension if it were right on top of beam or under the beam, but since point A is 'on the side' of the beam, how would you determine if its in compression or not?

I haven't included load P when imagining the forces acting on point A. I've just visualised b1 as a simple beam.
 
jack action said:
The moments (and forces) have directions that can be determined by the sign.

But for a beam in bending, you have the following situation:


When under the bending moment ##M##, the point on the convex portion (bottom) of the beam is in tension, but the concave portion (top) of the beam is in compression. The point A of your crankshaft would be in the concave portion.


Thanks. I completely forgot I had learned this... Thanks for refreshening my memory.

Someone has kindly pointed out that I have attached two images... Could you tell I'm new? Correct me if I am wrong, but if I were the find the stress at point A in the second image (greyed out one), point A would be in the concave portion and so be in tension, as the load P is now driving downwards instead of sideways?
 
Yes, in the greyed out image, point A would be in tension.

It is not a question of 'top' or 'bottom', it's a question of 'concave' and 'convex'. So it works in any position. Just imagine your part made out of rubber and imagine how it would deform under your load. If you're pulling on the handle (in any direction), the concave shape of the beam will be on the side that you are pulling, thus in compression.
 
yonese said:
Thank you! I hadn't thought of eliminating section b2, which does make it simplier to understand the forces acting on the beam. I can understand whether point A would be in compresssion or tension if it were right on top of beam or under the beam, but since point A is 'on the side' of the beam, how would you determine if its in compression or not?

I haven't included load P when imagining the forces acting on point A. I've just visualised b1 as a simple beam.
For figure Q5, point A would be under compression load, which would be the opposite to the situation shown in the greyed diagram.
 
Point A in your first diagram Figure 1 is not in the same place as point A in your second diagram Figure Q5.
 
  • Like
Likes   Reactions: Lnewqban

Similar threads

Engineering Crane at 45-degree angle supports load -- Find principal boom stresses
  • · Replies 7 ·
Replies
7
Views
3K
Engineering Combined loading, where is the neutral axis?
  • · Replies 11 ·
Replies
11
Views
3K
Engineering FEA Results interpretation for these 3 simulations
  • · Replies 8 ·
Replies
8
Views
2K
Maximum and minimum tensile/compressive strain in beam
  • · Replies 15 ·
Replies
15
Views
7K
Questions to do with crankshaft of an engine
  • · Replies 32 ·
2
Replies
32
Views
8K
Engineering Mechanics of Materials: find combined loading
  • · Replies 7 ·
Replies
7
Views
3K
Engineering Loads on a shaft with V-Belts
  • · Replies 2 ·
Replies
2
Views
3K
Engineering Shear stress problem: What decides the sign of Tau_V?
  • · Replies 2 ·
Replies
2
Views
2K
How Does Shear Stress in Beams Relate to Compression and Tension?
  • · Replies 6 ·
Replies
6
Views
4K
Engineering Bending Moment for Simply Supported, Overhanging Beam with two Overhangs
  • · Replies 4 ·
Replies
4
Views
3K