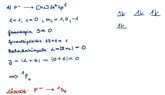physicisttobe
- 56
- 13
- Homework Statement
- electron configuration of SC
- Relevant Equations
- ...
I've solved further Term Symbol problems. The task is: derive the term symbols of the ground states of the following atoms: a) H, b) F, c) Cu, d) F- , e) P, f) Na, g) Sc
Why is the d-orbital considered here in g)? Why isn't the s orbital taken into account here? The 4s orbital is energetically higher than the 3d orbital, so why don't you look at the 4s orbital. I also post the solution and my approach to this problem. I can't explain why my approach is incorrect. Can someone help me?
my approach:
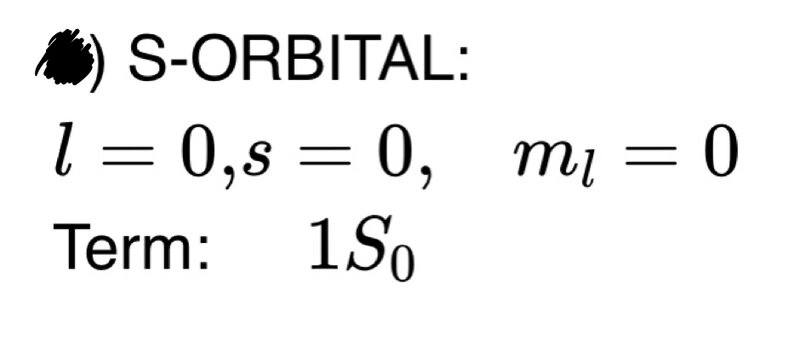
solution:
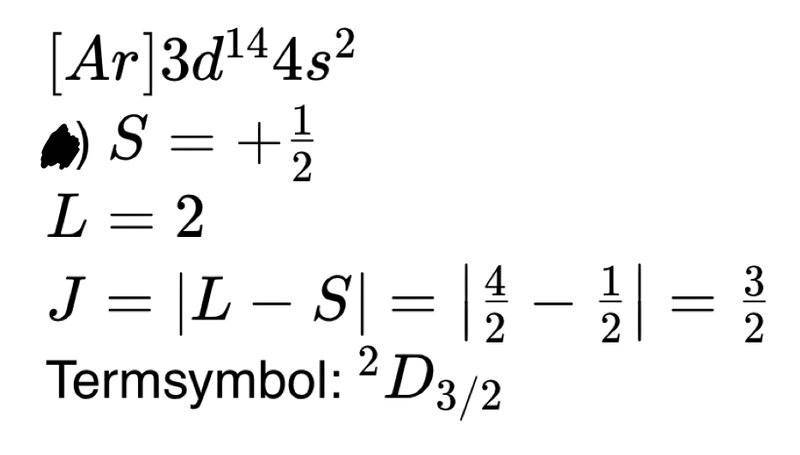
Why is the d-orbital considered here in g)? Why isn't the s orbital taken into account here? The 4s orbital is energetically higher than the 3d orbital, so why don't you look at the 4s orbital. I also post the solution and my approach to this problem. I can't explain why my approach is incorrect. Can someone help me?
my approach:
solution: