Why is the Highlighted Statement True?

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

Can someone please explain to me why the highlighted statement true?

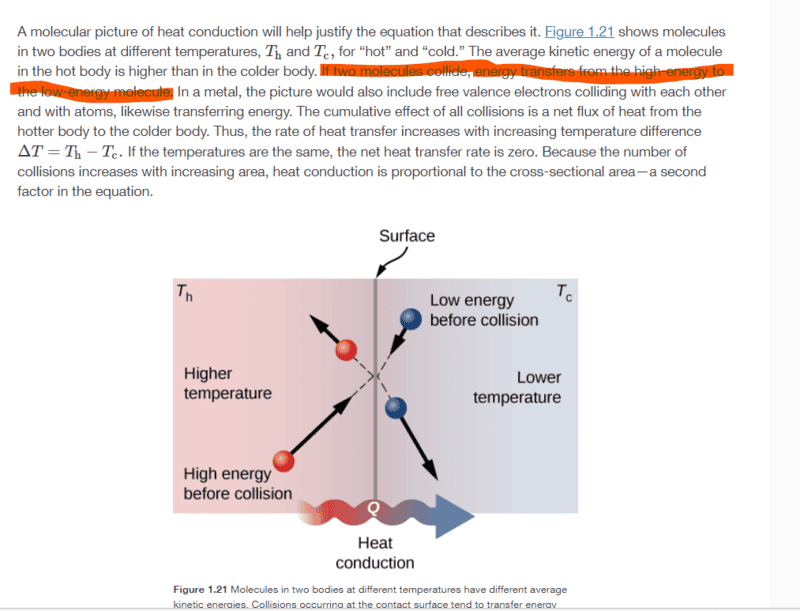
Many thanks!

 

[haruspex]

Simple kinetics. Consider two equal masses head-on in a perfectly elastic collision. Can you write the equations for the resulting velocities?

 

[member 731016]

Simple kinetics. Consider two equal masses head-on in a perfectly elastic collision. Can you write the equations for the resulting velocities?

Thank you for your reply @haruspex!

I guess it is reasonable assumption to assume that the molecules have the same mass.

$KE_i = KE_f$ for perfectly elastic collision
$\frac{1}{2}mv^2_{1i} + \frac{1}{2}mv^2_{2i} = \frac{1}{2}mv^2_{1f} + \frac{1}{2}mv^2_{2f}$
$mv^2_{1i} + mv^2_{2i} = mv^2_{1f} +mv^2_{2f}$
$v^2_{1i} + v^2_{2i} = v^2_{1f} +v^2_{2f}$

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex!

I guess it is reasonable assumption to assume that the molecules have the same mass.

$KE_i = KE_f$ for perfectly elastic collision
$\frac{1}{2}mv^2_{1i} + \frac{1}{2}mv^2_{2i} = \frac{1}{2}mv^2_{1f} + \frac{1}{2}mv^2_{2f}$
$mv^2_{1i} + mv^2_{2i} = mv^2_{1f} +mv^2_{2f}$
$v^2_{1i} + v^2_{2i} = v^2_{1f} +v^2_{2f}$

Many thanks!

and what about momentum conservation?

 

[Tom.G]

Or, some down-to-earth comments.

Have you played or watched a game of pool or billiards?
Have you ever witnessed a car collision where a car hits a stopped car?

Is there any movement of the stopped object when it is hit?

 

[haruspex]

Or, some down-to-earth comments.

Have you played or watched a game of pool or billiards?
Have you ever witnessed a car collision where a car hits a stopped car?

Is there any movement of the stopped object when it is hit?

ok, except that the statement under consideration appears to claim it as general fact, not as merely typical.

 

[member 731016]

Thank you for your replies @haruspex and @Tom.G !

$mv_{1i}+ mv_{2i} = mv_{1f}+ mv_{2f}$
$v_{1i}+ v_{2i} = v_{1f}+ v_{2f}$

 

[haruspex]

Thank you for your replies @haruspex and @Tom.G !

$mv_{1i}+ mv_{2i} = mv_{1f}+ mv_{2f}$
$v_{1i}+ v_{2i} = v_{1f}+ v_{2f}$

You should be able to combine the momentum and energy conservation laws to obtain: $v_{1i}- v_{2i} = v_{2f} -v_{1f}$. (This is even if the masses differ, and is a very useful equation to remember. There's also a more general form involving coefficient of restitution.)
What does that allow you to deduce when the masses are the same?

 

[member 731016]

You should be able to combine the momentum and energy conservation laws to obtain: $v_{1i}- v_{2i} = v_{2f} -v_{1f}$. (This is even if the masses differ, and is a very useful equation to remember. There's also a more general form involving coefficient of restitution.)
What does that allow you to deduce when the masses are the same?

Thank you for your reply @haruspex!

That equation says that the relative velocities of the masses before the collision is equal to the relative velocities of the masses after the collision when all velocities are taken from the same frame of reference. If the masses are the same, then initial relative KE will equal to the finial relative KE.

$KE_{{rel}_{i}} = KE_{{rel}_{f}}$
$\frac{2m}{2}(v_{1i}- v_{2i})^2 = \frac{2m}{2}(v_{2f} -v_{1f})^2$
$m(v_{1i}- v_{2i})^2 =m(v_{2f} -v_{1f})^2$
$(v_{1i}- v_{2i})^2 =(v_{2f} -v_{1f})^2$

Do you please know whether that was what I was meant to get?

Many thanks!

 

[haruspex]

Do you please know whether that was what I was meant to get?

No.
We have $v_{1i}- v_{2i} = v_{2f} -v_{1f}$ and the momentum conservation equation $m_1v_{1i}+ m_2v_{2i} = m_1v_{1f}+ m_2v_{2f}$. For the special case of equal masses, the latter reduces to:

$v_{1i}+ v_{2i} = v_{1f}+ v_{2f}$

What do those two equations that only involve velocities tell you?

 

[malawi_glenn]

$v_{1i}^2 + v_{2i}^2 = v_{1f}^2 + v_{2f}^2$ (1)
$v_{1i} + v_{2i} = v_{1f} + v_{2f}$ (2)

You should be able to reforumulate eq. (1) using the conjugate rule in order to invoke eq. (2) to get the velocitiy-relation that haruspex wrote.

 

[malawi_glenn]

ok, except that the statement under consideration appears to claim it as general fact, not as merely typical.

So? You also considered a special case, heads on collision.

 

[haruspex]

So? You also considered a special case, heads on collision.

That was a first step. The generalisation to oblique collisions is easy: just take the velocity components in the line of centres.
More problematic may be differing masses.

 

[malawi_glenn]

That was a first step. The generalisation to oblique collisions is easy: just take the velocity components in the line of centres.
More problematic may be differing masses.

But having one mass at rest initially is just to transform to its rest-frame

 

[haruspex]

But having one mass at rest initially is just to transform to its rest-frame

The distribution of KE looks different in different inertial frames. Two observers may disagree on which started with the greater KE. Yes, they will agree that the roles swapped, but this is likely to make the argument unconvincing to some.

 

[member 731016]

Thank you for your replies @haruspex and @malawi_glenn !

Sorry I will come back to this thread once the mid-term exams are over. I also don't want to waste your time on things I that are already in the textbook, so I think I will also finish learning momentum before replying.

Many thanks!