- #1
ChiralSuperfields
- 1,238
- 133
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
According to this,

The heat added to the system is proportional to the mass. Does someone please know how that highlighted statement is so? I think it is because the heat increases the internal energy of a system and internal energy is the sum of the translational, rotational, and vibrational kinetic energies and also potential energy (I'm not sure what types thought). Therefore, the mass of the system should increase since the particles will have more mechanical energy.
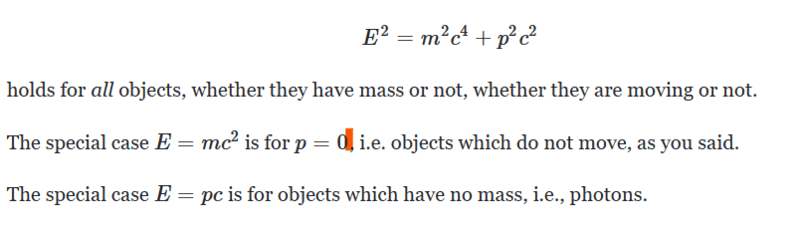
Many thanks!
The heat added to the system is proportional to the mass. Does someone please know how that highlighted statement is so? I think it is because the heat increases the internal energy of a system and internal energy is the sum of the translational, rotational, and vibrational kinetic energies and also potential energy (I'm not sure what types thought). Therefore, the mass of the system should increase since the particles will have more mechanical energy.
Many thanks!