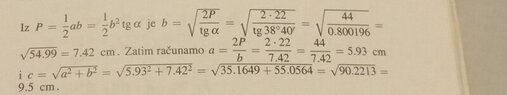Callmelucky
- 144
- 30
- Homework Statement
- Given the surface area of the right triangle = 22 cm^2 and one of his angles is 38°40'.
Calculate his other sides.
- Relevant Equations
- A=ab/2, tan(38°40')=b/a
so basically, here is a photo from the textbook(in attachments) and I'll write here how I did it. In my opinion, results should have been the same, but for some reason, they differ. So, if anyone can tell me what I am doing wrong I would appreciate it since I can't find mistakes caused by wrong calculations then it must be something conceptual that does not apply here, which is weird.
This is how I did it:
##A=\frac{ab}{2}## I wrote one side(b) using angle and the other side(a) like this: tan(38°40')=b/a --> 0.8a=b and then I plugged that in the formula for the surface of the triangle, after which I got b= 7.42. Which is the same as in solutions, this second part is what confuses me.
To calculate a, I just plugged b in 0.8a=b and got a=9.28. But in the textbook, b is plugged back in the formula for triangle surface and they got a = 5.93. After that our hypotenuses differ as well(obviously).
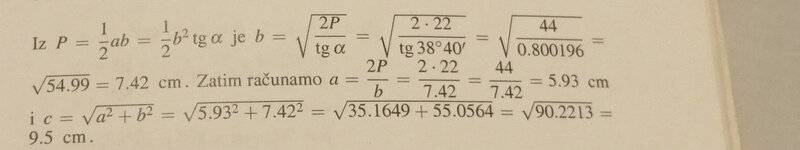
This is how I did it:
##A=\frac{ab}{2}## I wrote one side(b) using angle and the other side(a) like this: tan(38°40')=b/a --> 0.8a=b and then I plugged that in the formula for the surface of the triangle, after which I got b= 7.42. Which is the same as in solutions, this second part is what confuses me.
To calculate a, I just plugged b in 0.8a=b and got a=9.28. But in the textbook, b is plugged back in the formula for triangle surface and they got a = 5.93. After that our hypotenuses differ as well(obviously).
Last edited by a moderator: