Why P = F*v = ε^2/R = (vBl)^2/R when there's no friction?

In summary, the conversation discusses a problem involving a closed conductor loop in a magnetic field with a constant force acting on it. Using Faraday's law and Ohm's law, the current, force, and power in the circuit can be calculated. Ultimately, it is shown that the power formula (P = F*v) can be derived from the formula for speed and the formula for force on a conductor slice.
  • #1
Karagoz
52
5

Homework Statement


This is taken from a problem with its solution. But there's one thing I didn't understand with the solution:

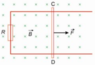
upload_2018-3-10_15-51-41.png


A closed conductor loop is located perpendicular to the field lines in a homogeneous magnetic field B. The conductor slice CD is first in rest. Then we pull a constant force F to the right. See figure above. The absolute value of the force is 1.8 N. The conductor slice slides without friction.

After a while the speed v is constant and is equal to 4.0 m/s. The length of the conductor slice CD is 12 cm.

The electrical power in the circuit is given by:
upload_2018-3-10_16-14-27.png


The effect of the pull force F is given by: P = F*v

Since we do not have friction, these powers must be the same. And this gives:
upload_2018-3-10_16-15-32.png


How is it that the effect on the pull force P = F*v is equal to the electrical power in the circuit given by:
upload_2018-3-10_16-14-27.png
?

What's the proof?

Homework Equations


P = F*v

P = ε^2/R = (vBl)^2/R

The Attempt at a Solution

[/B]
 

Attachments

  • upload_2018-3-10_15-51-41.png
    upload_2018-3-10_15-51-41.png
    11.9 KB · Views: 632
  • upload_2018-3-10_16-14-27.png
    upload_2018-3-10_16-14-27.png
    975 bytes · Views: 341
  • upload_2018-3-10_16-15-32.png
    upload_2018-3-10_16-15-32.png
    860 bytes · Views: 318
Physics news on Phys.org
  • #2
You can calculate the current ##I## from Faraday's Law. You can then do two separate calculations, (a) find the force from ##F=IlB## and (b) find the power dissipated in the resistor from ##P=I^2R##. If you put the two expressions side by side, you will see that ##I^2R = Fv##.

On edit: When the rod is moving at constant speed (terminal velocity), the net force on it is zero, and that's when the magnetic force ##IlB## matches the externally applied constant force ##F##.
 
Last edited:
  • #3
kuruman said:
You can calculate the current ##I## from Faraday's Law. You can then do two separate calculations, (a) find the force from ##F=IlB## and (b) find the power dissipated in the resistor from ##P=I^2R##. If you put the two expressions side by side, you will see that ##I^2R = Fv##.

On edit: When the rod is moving at constant speed (terminal velocity), the net force on it is zero, and that's when the magnetic force ##IlB## matches the externally applied constant force ##F##.

But how can we find current using Faraday's law? We can only find ε using Faraday's induction formula.

How is P = F*v derived form P = I^2*R in this case?
 
  • #4
Karagoz said:
But how can we find current using Faraday's law?
Using Ohm's law.
Karagoz said:
How is P = F*v derived form P = I^2*R in this case?
What did you not understand in #2?
 
  • #5
(I use capital L instead of l to make it easier to read).

Power formula: P = U^2/R

Faraday's law: U = vBL (I use U instead of ε)

Into the power formula:
P = (vBL)^2 / R

Formula for speed from Faraday's formula:
U = vBL
v = U/BL

Formula for the force on a conductor slice:
F = ILB

Current:
I = U/R

Into the formula for the force:
F = U/R * LB = ULB/R

Both the speed and power formula into the speed formula:
F*v = U/BL * ULB/R = U^2/R = P.

P = F*v = U^2/R.
 
  • #6
Karagoz said:
(I use capital L instead of l to make it easier to read).

Power formula: P = U^2/R

Faraday's law: U = vBL (I use U instead of ε)

Into the power formula:
P = (vBL)^2 / R

Formula for speed from Faraday's formula:
U = vBL
v = U/BL

Formula for the force on a conductor slice:
F = ILB

Current:
I = U/R

Into the formula for the force:
F = U/R * LB = ULB/R

Both the speed and power formula into the speed formula:
F*v = U/BL * ULB/R = U^2/R = P.

P = F*v = U^2/R.
Looks good!
Is there any question?
 
  • #7
cnh1995 said:
Looks good!
Is there any question?

No, I got it. thanks
 

FAQ: Why P = F*v = ε^2/R = (vBl)^2/R when there's no friction?

What does P = F*v = ε^2/R = (vBl)^2/R mean?

This equation is known as the power equation and it relates power (P) to force (F), velocity (v), electric field (ε), and resistance (R). It states that power is equal to the product of force and velocity, as well as the square of electric field divided by resistance and the square of velocity multiplied by magnetic field (B) and length (l) divided by resistance.

Why is there no friction in this equation?

This equation assumes a frictionless environment, meaning there is no resistance or friction acting against the motion of the object. This is often used in theoretical physics problems to simplify calculations.

How is P = F*v = ε^2/R = (vBl)^2/R derived?

This equation is derived from the basic principles of work, power, and energy. Power is defined as the rate at which work is done, and work is equal to force multiplied by distance. Additionally, the electric field is defined as the force per unit charge, and Ohm's law states that current (I) is equal to electric field divided by resistance. By substituting these equations into the power equation, we arrive at P = F*v = ε^2/R = (vBl)^2/R.

What is the significance of P = F*v = ε^2/R = (vBl)^2/R in physics?

This equation is significant because it relates various physical quantities that are fundamental to understanding the behavior of objects in motion. It also highlights the relationship between electricity and magnetism, as well as the concept of energy conservation.

Can this equation be applied in real-world situations?

Yes, this equation can be applied in real-world situations as long as the assumptions of a frictionless environment and ideal conditions are met. However, in most cases, there will be some level of friction or resistance, so the equation may need to be modified to account for these factors.

Similar threads

When is power constant in this scenario?
Replies
25
Views
1K
Find the power needed to accelerate this elevator downward
Replies
4
Views
1K
Find the velocity and strength of magnetic field from the given info
Replies
4
Views
10K
Conflict in formulas P = IR^2 and P=delta v/r
Replies
19
Views
2K
P= F(t) • V(t) vs P = F • V to find power done
Replies
2
Views
1K
Multiple choice Q: Mangetic fields and Spring Constant
Replies
8
Views
2K
Power of Boat: Exploring R vs F
Replies
2
Views
3K
What is the induced magnetic force on this closed current loop?
Replies
12
Views
943
Why can we move the spring with constant speed when we apply a force?
Replies
29
Views
2K
Optimizing Voltage for Power Transmission Efficiency
Replies
4
Views
4K

Hot Threads

Recent Insights

Back
Top