Why to write numbers in square roots and not in decimals?

[pairofstrings]

Hi. I have coefficient of x² as

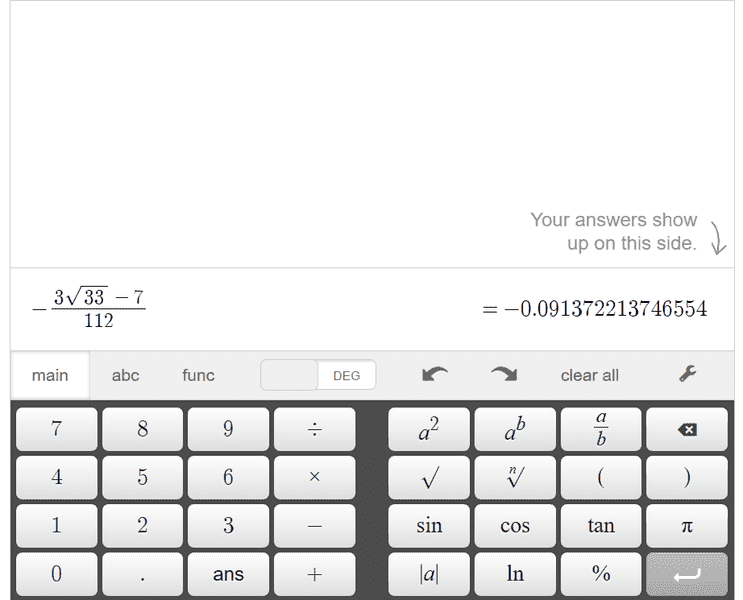
in an expression that looks like this

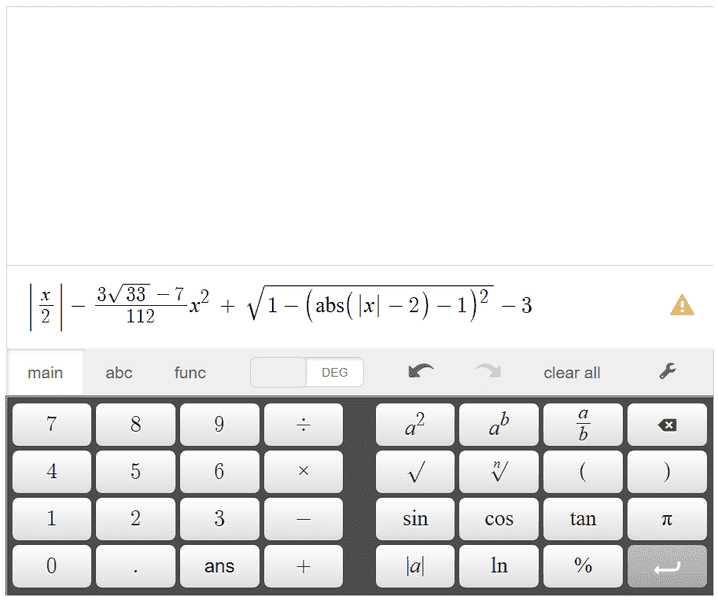
* calculator shows little yellow triangle because 'x' is not defined.

If I can write the coefficient of x² as - 0.091372213746554 then why did the author write coefficient of x² like this shown below?

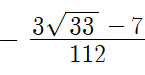
Thanks.

 

[jtbell]

the author

Of what?

 

[mfb]

-0.091372213746554 is not exact. It is only an approximation, where the number of digits is determined by the the calculator. A better approximation is:
-0.091372213746554339103141378613 - but that is again not exact, it just has a smaller error. No matter how many digits you add you always have an error.

$\displaystyle -\frac{3\sqrt{33}-4}{112}$ is exact.

 

[pairofstrings]

Of what?

Sorry.
The author is https://www.desmos.com/calculator/dnzfajfpym and expression is at serial number 3.

 

[Mark44]

@pairofstrings, you seem to have a fundamental misunderstanding of the difference between numbers represented by radicals and decimal approximations of them. For example, the exact value of the diagonal of a square 1 unit on each side is $\sqrt 2$. This value can be approximated by 1.414 or 1.4142 or 1.41421 or even 1.4142135623730950488016887242097, but none of them is exactly equal to $\sqrt 2$.

$\sqrt 2$ is an example of an irrational number, one whose decimal represention takes an infinite number of digits to the right of the decimal point, with no repeating pattern.