- #1
- 37,622
- 9,857
I ran into an interesting video on Youtube yesterday, about a fast way to compute the reciprocal of the square root of a number. I.e., to compute this function:
##f(x)= \frac 1 {\sqrt x}##
The presenter is John Carmack. If you search for "Fast Inverse Square Root — A Quake III Algorithm" you'll find it.
The video shows a technique used in Quake III to speed up the calculations for lighting and reflections, to normalize vectors to a magnitude or length of 1.
The obvious way to do the calculation as a C function might be as follows:
Such a function would produce correct values, within the limits of the float data type, but would be extremely slow. A very clever programmer at Quake came up with the following version.
I have modified the code shown in the video slightly, changing the name of the function and removing one comment that was an acronym I don't wish to write here. Most of the code is very arcane, with no comments that explain what the code is doing. For a full explanation of how the code works, take a look at the video, starting at about 10 minutes.
I put together a program with the above function. In it I compared the resulting times to calculate the reciprocal square roots of several numbers in an array of floats using both the obvious (but slow) approach I showed first, as well as the function shown just above. My results confirmed that the Quake III algorithm is very fast, producing results that were within 1%, and taking a little over one-hundredth of the time.
Here's the output I got with an array of 10 float values:
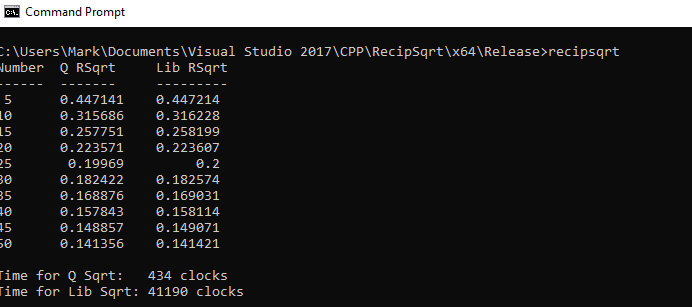
The first column shows the numbers in the array, 5.0 through 50.0, in increments of 5.0. The second column shows the values produced by the Quake algorithm, and the third column shows the values produced using the standard library sqrt() function.
The two lines at the bottom show the elapsed time, in clock ticks (AKA "clocks") for each algorithm. My 8-year-old computer runs at 3.4 GHz, so by my calculation, 434 clocks works out to 127.6 nsecs.
I wrote the program in Visual Studio 2017, in x64 Release mode, with optimization turned on to Max Optimization favoring speed, but even so, the Quake algorithm outperformed the intuitively obvious algorithm by two orders of magnitude.
In case you're curious about how I did the timing, I have a small assembly routine that I include as a separate file in my project. The assembly routine uses 64-bit registers, which is why I compiled the program as a 64-bit program. Doing so also meant that I had to have a separate assembly file rather than using inline assembly, which can be done only for 32-bit programs.
Here's my timing routine:
The rdtsc instruction (Read Time Stamp Counter) gets the current time as a 64 bit number, spread out in the 32-bit EDX and EAX registers. The remaining instructions combine the two values into the 64-bit RAX register.
##f(x)= \frac 1 {\sqrt x}##
The presenter is John Carmack. If you search for "Fast Inverse Square Root — A Quake III Algorithm" you'll find it.
The video shows a technique used in Quake III to speed up the calculations for lighting and reflections, to normalize vectors to a magnitude or length of 1.
The obvious way to do the calculation as a C function might be as follows:
C:
#include <math.h>
float RecipSqrt(float num) {
return 1/sqrt(num);
}
C:
float RecipSqrt(float number)
{
long i;
float x2, y;
const float THREEHALVES = 1.5F;
x2 = number * 0.5F;
y = number;
i = *(long*)&y; // Evil floating point bit hack
i = 0x5f3759df - (i >> 1);
y = *(float*)&i;
y = y * (THREEHALVES - (x2 * y * y)); // 1st iteration
return y;
}I put together a program with the above function. In it I compared the resulting times to calculate the reciprocal square roots of several numbers in an array of floats using both the obvious (but slow) approach I showed first, as well as the function shown just above. My results confirmed that the Quake III algorithm is very fast, producing results that were within 1%, and taking a little over one-hundredth of the time.
Here's the output I got with an array of 10 float values:
The first column shows the numbers in the array, 5.0 through 50.0, in increments of 5.0. The second column shows the values produced by the Quake algorithm, and the third column shows the values produced using the standard library sqrt() function.
The two lines at the bottom show the elapsed time, in clock ticks (AKA "clocks") for each algorithm. My 8-year-old computer runs at 3.4 GHz, so by my calculation, 434 clocks works out to 127.6 nsecs.
I wrote the program in Visual Studio 2017, in x64 Release mode, with optimization turned on to Max Optimization favoring speed, but even so, the Quake algorithm outperformed the intuitively obvious algorithm by two orders of magnitude.
In case you're curious about how I did the timing, I have a small assembly routine that I include as a separate file in my project. The assembly routine uses 64-bit registers, which is why I compiled the program as a 64-bit program. Doing so also meant that I had to have a separate assembly file rather than using inline assembly, which can be done only for 32-bit programs.
Here's my timing routine:
C:
.code
readCurrentTime PROC C
;; Returns the start time, clocks, in RAX.
rdtsc
shl rdx, 32
or rax, rdx
ret
readCurrentTime ENDP
end
Last edited:
