Wire loop in magnetic field of the long magnet

[sergiokapone]

Homework Statement

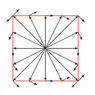
The wire loop $ABCD$ is in a magnetic field of the long thin rod magnet with a magnetic moment per unit volume of $\mathfrak{M}_0$ and a cross section $S$. The north pole of this magnet is in the center of the loop, and the magnet is perpendicular to the plane of the loop. Emf is connected to the opposite edges of the diagonal $AC$ , thus the current I is flow along sides of the circuit. Find the torque of force couple M and its direction.

Homework Equations

[/B]

The Attempt at a Solution

The magnet field of the long magnet near the north pole one can represent as magnetic field of monopole
\begin{equation}
H = \frac{q_m}{r^2}
\end{equation}




where $q_m$ -- effective magnetic charge, which one can find from definition of magnetic momentum $p_m = q_ml$:
\begin{equation*}
q_ml = \mathfrak{M}_0 S l
\end{equation*}
thus, the effective magnetic charge is
\begin{equation}
q_m = \mathfrak{M}_0 S.
\end{equation}

The Ampere Force acting on sides of wire loop:
\begin{equation}
dF = Idl H \sin\alpha,
\end{equation}
And, so the torque is
\begin{equation}
M = \int rdF = I\mathfrak{M}_0 S \int \frac{\sin\alpha}{r} dl
\end{equation}
from the geometry $dl\sin\alpha = r d\alpha$, thus

\begin{equation}
M = \int rdF = I\mathfrak{M}_0 S 4 \frac{\pi}{2}
\end{equation}

The answer in the problems book is
\begin{equation}
M = \int rdF = 4 I\mathfrak{M}_0 S
\end{equation}

Where did I go wrong?

 

[TSny]

I believe you haven't taken into account the direction of the torque, $\vec{dM} = \vec{r} \times \vec{dF}$, for each element of current $dl$.

 

[sergiokapone]

TSny, but $\vec r \bot \vec{dF}$, thus $\left| \vec{dM} \right| = rdF$.[PLAIN]https://www.physicsforums.com/members/tsny.229090/[/PLAIN]

 

[sergiokapone]

Illustration for solution

 

[BvU]

TSny, but $\vec r \bot \vec{dF}$, thus $\left| \vec{dM} \right| = rdF$.

That's right, but what TS says is that not all $\vec {dM}$ are pointing in the same direction !

 

[sergiokapone]

Ok,I lost sight of that, thanks. In the process of integration one will have to take into account the changes in the angles between the current and the radius vector, and count the direction of torque also. Tedious way.

Is there a more general way? (I mean using only vectors)
May be, an easier way:
\begin{equation}
\vec M = I \oint \vec{dl} (\vec B \cdot \vec r) - \vec B (\vec r \cdot \vec{dl}).
\end{equation}

But following using Stokes' theorem $I \oint_L \vec{dl} =I \int_S \vec{dS} \times \nabla$ I get zero.

 

[TSny]

If you look at all the torque elements, you can see that the net torque vector is in a certain direction. So, you can just sum the torque components in that direction.