Lo.Lee.Ta.
- 217
- 0
Okay, I tried to draw a picture of the graph the word problem is talking about.
This is a bad picture, but it was the best my computer could take! :/
1. Les triangles dangereux is an 80-minute movie showing nothing but a slowly growing triangle.
It got a strong reception at Cannes, and is now opening in the US.
For the whole movie, the triangle lies between the x-axis and the line y = 5x + 100, with the left side at the intersection of these lines; but the right side of the triangle grows throughout the movie.
Specifically, at time t minutes into the movie, the right side of the triangle is the line x = t. So, for example, what's going on at various times throughout the movie is shown in the four pictures below.
a. Calculate the areas of each of these triangles. Don't use Calculus.
b. Calculate the area A(t) of the triangle shown t minutes into the movie, as a function of t. Again, don't use Calculus.
c. Calculate the derivative dA/dt.
Be sure to use the correct variables! Variables aside, the derivative should
look just like the equation of the line. Without referring to the Fundamental Theorem of Calculus, explain carefully why these should look the same.
Hint: what does dA/dt mean? Think about it.
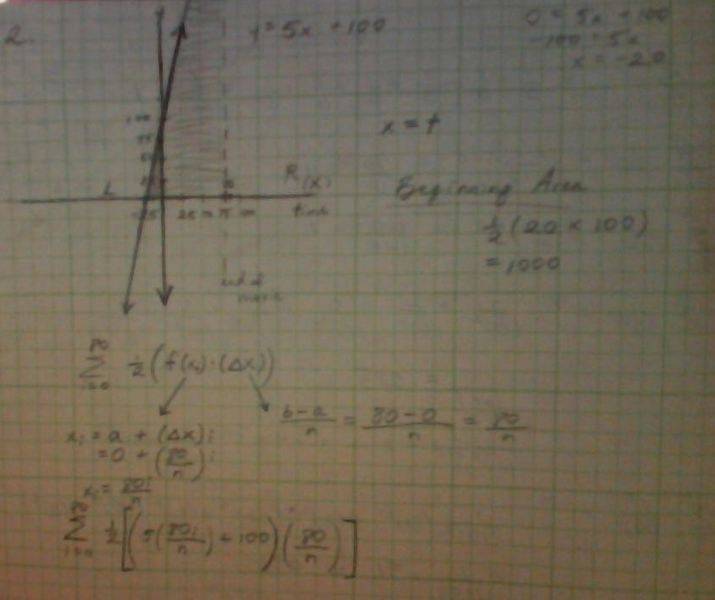
2.
a. For question a, I'm confused as to which triangles it wants me to find the area of...
Calculate the area of the triangle when it gets to 80min? Calculate that area of the traingle at the beginning?
Not sure...
b. So I think this question is just asking me to find the area of the triangle at any minute (but I have to call the minute I choose "t.")
For the graph, I thought that since x=t, the growing right-sided line of the triangle has to start at x=0. I gather that the line moves at a constant rate.
When time (t)= 1min, I thought also the triangle's right-sided line is at x=1.
The line would be at x=15 when 15min have passed.
Every minute that passes, the right-handed side of the triangle grows by 1.
Alright, since I cannot use Calculus to solve the problem, I thought I would have to use
a Riemann Sum.
I'll say time (t)= 15min.
So I'm trying to find the area of the triangle after 15min.
n
Ʃ [1/2(f(xi)*(Δx))]
i=0
I chose i=0 because the triangle starts growing at x=0.
I put n at the top because there are a bunch of little rectangles filling up the area, and I don't know how many of them there are.
Is this right so far...? :/
This is a bad picture, but it was the best my computer could take! :/
1. Les triangles dangereux is an 80-minute movie showing nothing but a slowly growing triangle.
It got a strong reception at Cannes, and is now opening in the US.
For the whole movie, the triangle lies between the x-axis and the line y = 5x + 100, with the left side at the intersection of these lines; but the right side of the triangle grows throughout the movie.
Specifically, at time t minutes into the movie, the right side of the triangle is the line x = t. So, for example, what's going on at various times throughout the movie is shown in the four pictures below.
a. Calculate the areas of each of these triangles. Don't use Calculus.
b. Calculate the area A(t) of the triangle shown t minutes into the movie, as a function of t. Again, don't use Calculus.
c. Calculate the derivative dA/dt.
Be sure to use the correct variables! Variables aside, the derivative should
look just like the equation of the line. Without referring to the Fundamental Theorem of Calculus, explain carefully why these should look the same.
Hint: what does dA/dt mean? Think about it.
2.
a. For question a, I'm confused as to which triangles it wants me to find the area of...
Calculate the area of the triangle when it gets to 80min? Calculate that area of the traingle at the beginning?
Not sure...
b. So I think this question is just asking me to find the area of the triangle at any minute (but I have to call the minute I choose "t.")
For the graph, I thought that since x=t, the growing right-sided line of the triangle has to start at x=0. I gather that the line moves at a constant rate.
When time (t)= 1min, I thought also the triangle's right-sided line is at x=1.
The line would be at x=15 when 15min have passed.
Every minute that passes, the right-handed side of the triangle grows by 1.
Alright, since I cannot use Calculus to solve the problem, I thought I would have to use
a Riemann Sum.
I'll say time (t)= 15min.
So I'm trying to find the area of the triangle after 15min.
n
Ʃ [1/2(f(xi)*(Δx))]
i=0
I chose i=0 because the triangle starts growing at x=0.
I put n at the top because there are a bunch of little rectangles filling up the area, and I don't know how many of them there are.
Is this right so far...? :/