Work done on a falling elevator by a spring + gravity

[simphys]

Homework Statement

An elevator cable breaks when a 925-kg elevator
is 22.5 m above the top of a huge spring
at the bottom of the shaft. Calculate
(a) the work done by gravity on the elevator before it hits the
spring; (b) the speed of the elevator just before striking the
spring; (c) the amount the spring compresses (note that here
work is done by both the spring and gravity).

Relevant Equations

WE principle + w=Fd

I don't understand what I have done wrong in part (c) I have the initial velocity for the second part of the motion and have the final velocity zero and then the net work done is W_mg + W_Fs and the actual answer for x is 2.37m
Could I get some help/tips please, thanks in advance.

Here is my solution

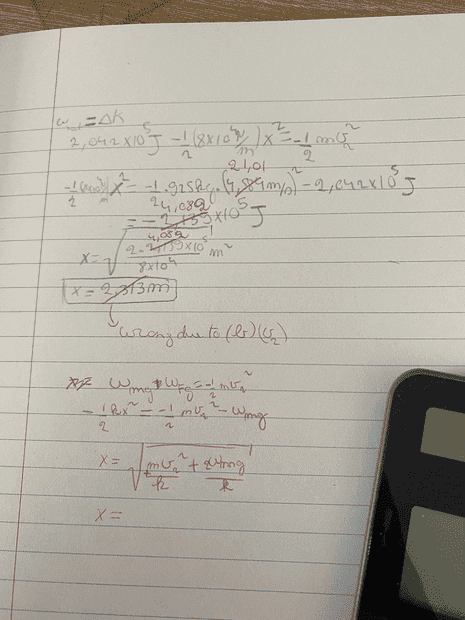
small edit: After getting V_2 = 21m/s, x = 3.19m and the ,(comma) is a decimal point here! .(dot) is multiplication

 

[simphys]

I think I see the problem.. I used the work done by gravity from the free fall motion part.
for the second part it actually is W_mg = mgx (if I am not mistaking)

 

[simphys]

I got the following: $-4E4*x^2 + 9.074E3*x + 2.04E5=0$
which I solved with the calculator directly, but using the quadractic formula would be a lot of writing, is there another way I can look at this problem or something?

 

[haruspex]

I got the following: $-4E4*x^2 + 9.074E3*x + 2.04E5=0$
which I solved with the calculator directly, but using the quadractic formula would be a lot of writing, is there another way I can look at this problem or something?

I cannot read the value of k in the posted image, but I deduce it must be 8E4 N/m.
I agree with your quadratic. There's no simpler approach.

 

[simphys]

I cannot read the value of k in the posted image, but I deduce it must be 8E4 N/m.
I agree with your quadratic. There's no simpler approach.

Thank you! I thought that there may be a way to just use the initial and final position instead of breaking it up into part, but I didn't try. I supposed that it might've work that is why I asked.

 

[haruspex]

Thank you! I thought that there may be a way to just use the initial and final position instead of breaking it up into part, but I didn't try. I supposed that it might've work that is why I asked.

Sorry, I thought you were just asking about solving the quadratic at the end.
Yes, if you only had to solve part c you could just write the conservation of energy equation straight off:
$(h+x)mg=\frac 12kx^2$
and get the quadratic from that.

 

[simphys]

Sorry, I thought you were just asking about solving the quadratic at the end.
Yes, if you only had to solve part c you could just write the conservation of energy equation straight off:
$(h+x)mg=\frac 12kx^2$
and get the quadratic from that.

Oh right, way faster thus. Thank you!