SUMMARY
The forum discussion centers on the relationship between force as a function of position and time, specifically questioning the validity of the equation F(x(t)) = m(a(t)). Participants clarify that x(t) represents displacement as a function of time, while F(x) and F(t) denote force as functions of position and time, respectively. The consensus is that dimensions must match in physically meaningful equations, leading to the conclusion that F(x(t)) ≠ F(t) due to differing dimensions. The discussion emphasizes the importance of correctly interpreting functions and their variables in physics.
PREREQUISITES
- Understanding of basic physics concepts such as force, mass, and acceleration.
- Familiarity with functions and their notation in mathematics.
- Knowledge of dimensional analysis in physics.
- Experience with calculus, particularly derivatives and their physical interpretations.
NEXT STEPS
- Study the concept of dimensional analysis in physics to ensure equations are dimensionally consistent.
- Learn about the relationship between force, mass, and acceleration in Newtonian mechanics.
- Explore the mathematical treatment of functions in physics, particularly how to express physical quantities as functions of different variables.
- Investigate the implications of using different notations for functions of time and position in physics.
USEFUL FOR
This discussion is beneficial for physics students, educators, and anyone interested in understanding the nuances of force equations and their applications in mechanics.

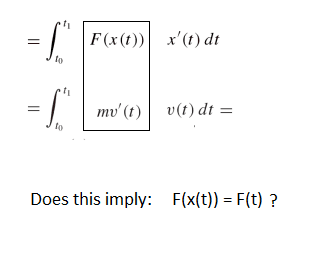 My best guess is that x(t) ≠ t
My best guess is that x(t) ≠ t