guyvsdcsniper
- 264
- 37
- Homework Statement
- A reversible refrigerator engine extracts heat from
the inside of a refrigerator compartment kept at 8°C and rejects unwanted
heat QH to its 20°C exterior. Find the work required to extract one calorie
from the interior of the refrigerator compartment
- Relevant Equations
- dQ/T=0
The answer key says the work done should be +.043cal. I am getting a negative sign.
I have posted my work in the attached image.
My logic is that since this a reversible engine we can say the integral of dQ/T=0. Looking at the cycle, Qc isi being absorbed (Qc>0) and Qh is being rejected (Qh<0). Then we can say Qc/Tc-Qh/Th=0.
Solving for Qh, we get 1.0427cal.
We also know W= the integral of dQ. So we can say W=Qc-Qh.
Doing so makes me get a negative sign.
I guess from my perspective the negative indicates the system is doing work, hence W<0.
Am I doing something wrong/looking at the situation from a different perspective by getting this negative sign?
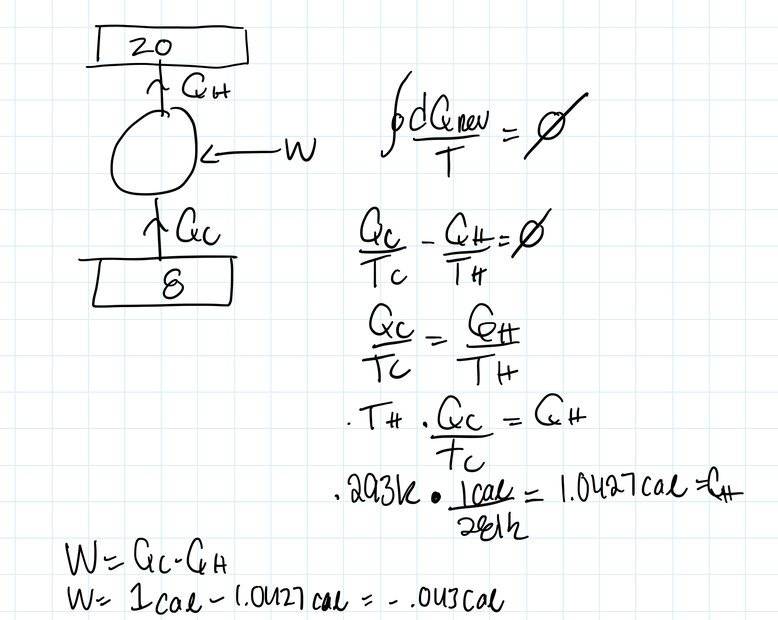
I have posted my work in the attached image.
My logic is that since this a reversible engine we can say the integral of dQ/T=0. Looking at the cycle, Qc isi being absorbed (Qc>0) and Qh is being rejected (Qh<0). Then we can say Qc/Tc-Qh/Th=0.
Solving for Qh, we get 1.0427cal.
We also know W= the integral of dQ. So we can say W=Qc-Qh.
Doing so makes me get a negative sign.
I guess from my perspective the negative indicates the system is doing work, hence W<0.
Am I doing something wrong/looking at the situation from a different perspective by getting this negative sign?